ПОМОГИТЕ,ПРОШУ!В треугольнике ABC известно, что угол C = 90 градусов, AC=BC=14 см. Две стороны квадрата CDEF лежат на катетах треугольника ABC а вершина E принадлежит гипотенузе AB.Найдите периметр квадрата.(ПОЖАЛУЙСТА С РИСУНКОМ И С КАЧЕСТВЕННЫМ ОБЪЯСНЕНИЯЕМ,В БАЛЛАХ НЕ ОБИЖУ!) кто нормально решит,тому дам ,,лучший ответ,,

АВ=АС=14,
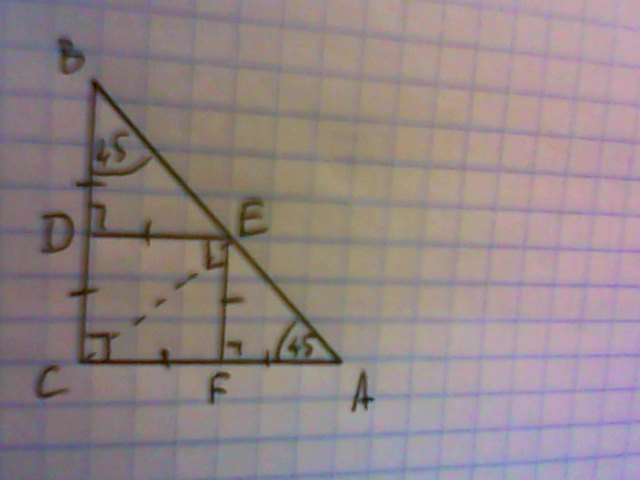
Биссектриса  угла С пересекает гипотенузу в точке Е, СЕ - является диагональю искомого квадрата, DЕ⊥ВС, FE⊥АС.
ΔВDЕ=ΔАFЕ, они прямоугольные, равнобедренные (углы по 45°)
У квадрата все стороны равны отсюда каждая сторона квадрата равна 
половине катета ΔАВС.
СD=DЕ=FE=FC=7.
Периметр  квадрата равен Р= 4·7= 28 линейных единиц.

дополню только, зачем нужна биссектриса. Т.к. точка Е должна быть равноудалена (квадрат ведь) от сторон CD и CF

Это для построения квадрата

это для доказательства того, где должна быть т.Е