Краткое доказательство признака параллельности плоскостей

Две прямые на плоскости называются параллельными, если они не имеют общих точек.
Две прямые в трехмерном пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.

Не увидел :D Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

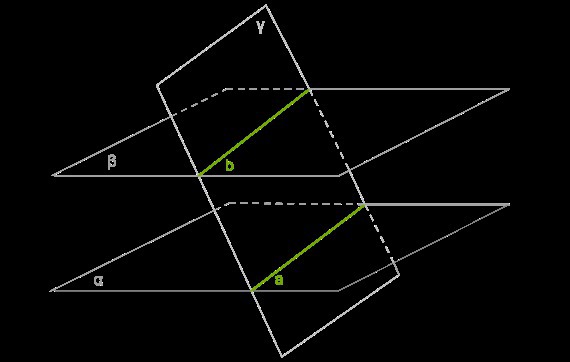
Пусть α и β - параллельные плоскости, а γ- плоскость, пересекающая их.
Плоскость α пересекается с плоскостью γ по прямой a.
Плоскость β пересекается с плоскостью γ по прямой b.

Линии пересечения a и b лежат в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

Не за что ;)