Предмет: Математика,
автор: marianna0715
ОЧЕНЬ СРОЧНО!!!!!! ПОМОГИТЕ!
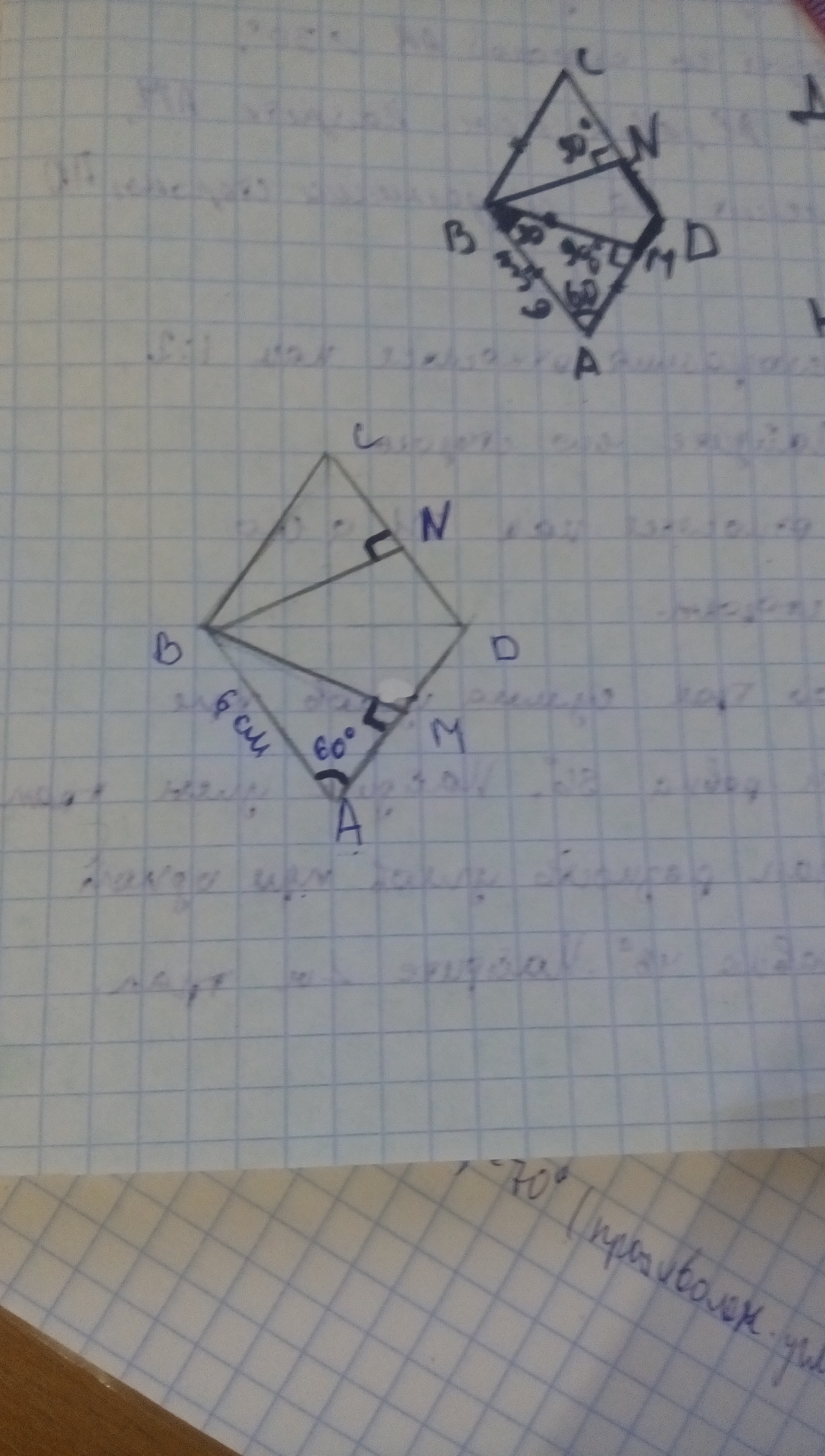
В ромбе ABCD угол А равен 60 градусов, сторона АВ=6 см. Из вершины В на тороны АD и СD проведены перпендикуляры BM и BN. Чему равна сумма сторон MD+DN
Приложения:
Ответы
Автор ответа:
0
Ответ:
MD+DN = 6 см.
Пошаговое объяснение:
Свойства ромба: в ромбе все стороны равны; в ромбе противолежащие углы равны.
1) Рассмотрим ΔABM.
BM ⊥ AD, ∠AMB = 90° по условию.
∠BAM = 60° по условию. ⇒ ∠ABM = 30°.
В прямоугольном треугольнике катет, лежащий против угла 30° равен половине гипотенузы. AM = BA / 2 = 6 см / 2 = 3 см.
2) AD = 6 см. Отрезок MD = AD - AM = 6 см - 3 см = 3 см.
3) Аналогично в ΔBCN.
BN ⊥ CD, ∠BNC = 90° по условию.
∠BCN = 60° ⇒ ∠CBN = 30°.
В прямоугольном треугольнике катет, лежащий против угла 30° равен половине гипотенузы. CN = CB / 2 = 6 см / 2 = 3 см.
Отрезок ND = CD - CN = 6 см - 3 см = 3 см.
4) Cумма отрезков MD + DN = 3 см + 3 см = 6 см.
Интересные вопросы
Предмет: Українська література,
автор: antondemch4554
Предмет: Русский язык,
автор: tvvovvv1
Предмет: Геометрия,
автор: pastusokdima512
Предмет: Физика,
автор: allahsnami