решите пожалуйста В2 В3 С1

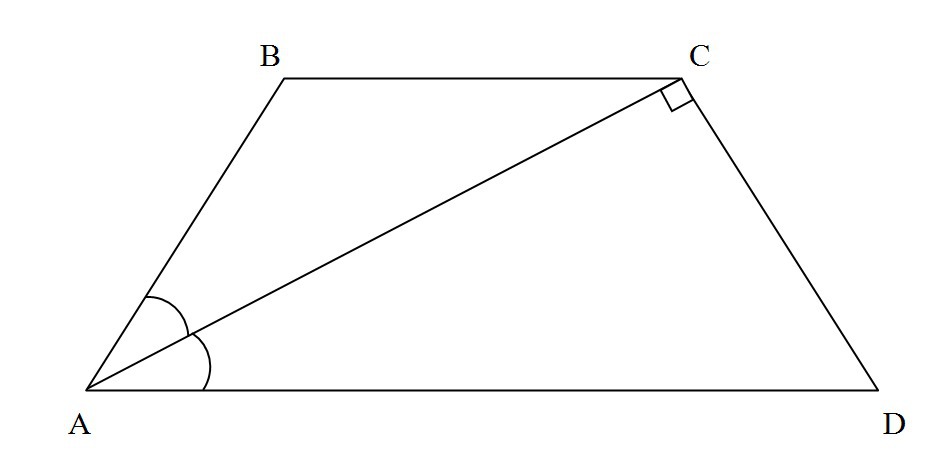
B2) В прямоугольном Δ АСD: ∠CDA=60° ∠ACD=90°  => ∠CAD=∠BAC = 30°
      
      Так как  ∠CAD +∠BAC = ∠BAD = 30+30 = 60°, то:
      трапеция ABCD - равнобедренная и АВ = CD.

      Из свойства прямоугольного треугольника, катет CD, лежащий
     напротив угла в 30°, равен половине гипотенузы AD.

     Углы ∠CAD = ∠ВСА, как накрестлежащие при параллельных ВС и AD и
     секущей АС.
    Следовательно, Δ АВС - равнобедренный и АВ = ВС

    Периметр трапеции Р = 35 см => 
       =>  35 = AB+BC+CD+AD = 3*AB + 2*AB = 5*AB
             AB = 35 : 5 = 7(см)

Ответ: 7 см      

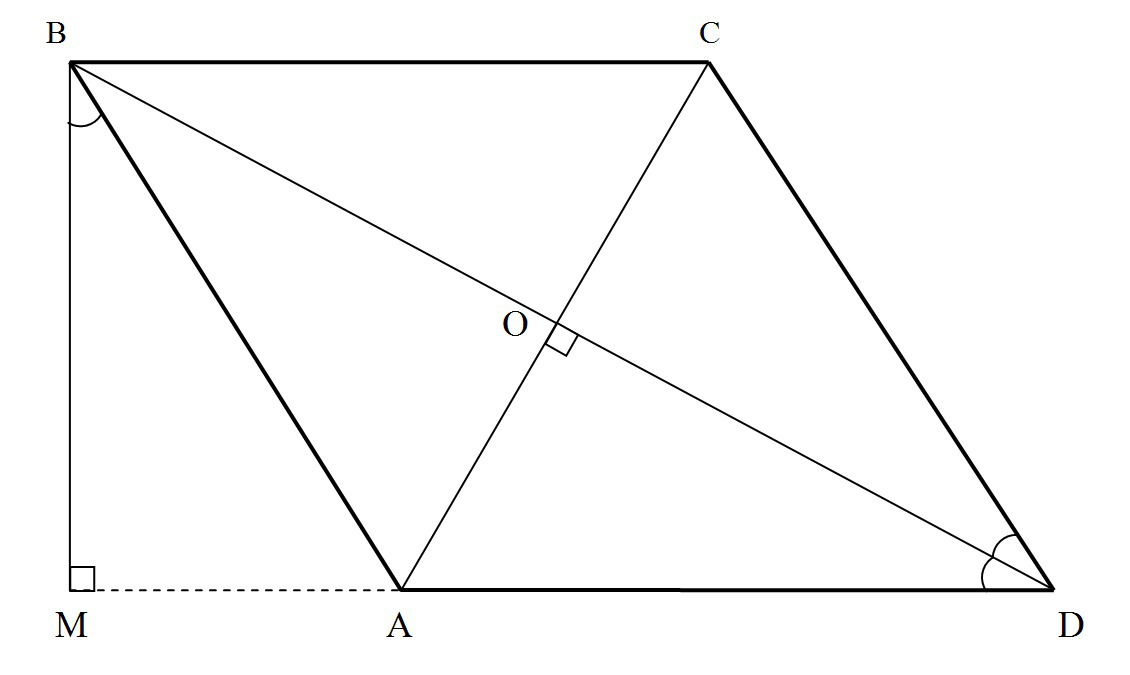
В3).  ABCD - ромб, СК⊥АD  AK=KD

       В ромбе все 4 стороны равны. => AD=CD

       В треугольниках АСК и СКD:    AK=KD, ∠CKD=∠CKA, СК - общая
       Значит, эти треугольники равны по первому признаку
       (двум сторонам и углу между ними).
       Следовательно,  СА=CD=AD и АСD - равносторонний => ∠CDA=60°

Ответ: 60°

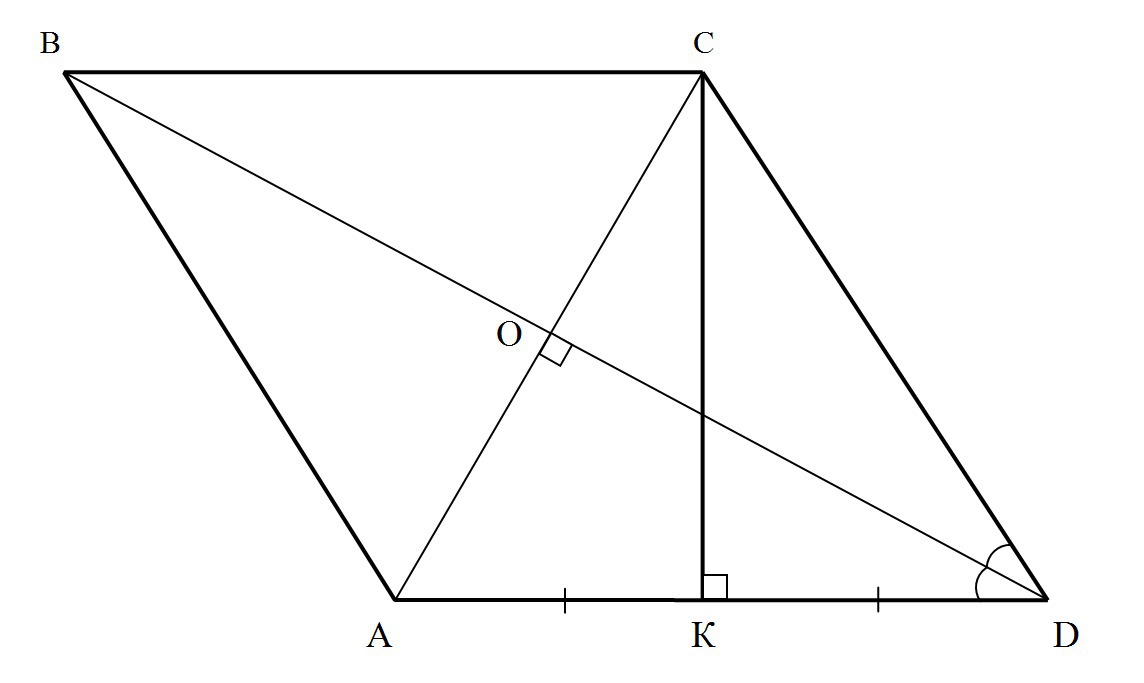
С1). Дано: ABCD - ромб, ВМ⊥MD,  ∠MBA=30°, AC =6 см 
        Найти: АМ = ?

Диагонали ромба пересекаются под прямым углом и делятся точкой пересечения пополам, а так же являются биссектрисами своих углов. => ∠АВО = ∠ОВС.

Так как ВС || MD и ВМ⊥MD, то: МВС = 90°
Тогда: МВС = ∠МВА+∠АВО+∠ОВС
              90 = 30 + 2*∠АВО
              ∠АВО = (90-30):2 = 30°
Так как АО лежит напротив угла в 30°, то: АВ = 2*АО = АС = 6 (см) 

В треугольнике МВА: катет МА лежит напротив угла в 30°
Следовательно:
                             МА = 0,5*АВ = 3 (см)

Ответ: 3 см

55..))

Нормально..)) У меня младшему сыну только 15 исполнилось...)) Хороший возраст!