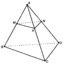
На ребрах DA, DB и DC тетраэдра DABC отмечены точки М, N и Р так, что DM:MA = DN:NB = DP:PC. Докажите, что плоскости MNP и ABC параллельны. Найдите площадь треугольника MNP, если площадь треугольника ABC равна 10 см2 и DM: МА = 2:1.

1) так как точки делят рёбра тетраэда на 2 равные части, то получится что и растояние в каждой точки плоскости NMP будет одинаково отдалено от плоскости ABC, следовательно они будут паралельны.
так как отношение ДМ к МА как 2 к 1, то и тетраэды будут относиться друг к другу как 2 к 1, следовательно основание АВС будет относиться к основанию МНП как 2 к 1 и получится что МНП=10*1/2=5 см².