Помогите плиз с тригонометрическим уравнением 2sin(x-П/2)•cos(П/2+x)+корень 3•cosx =0 на [-6П; -5П]

sin(x-(π/2))=-sin((π/2)-x) так как синус - нечетная функция.
По формулам приведения
sin((π/2)-x)=cosx
cos(П/2+x)=-sinx

2·(-cosx)·(-sinx)+√3cosx =0;
2·cosx·sinx+√3cosx =0;
cosx·(2sinx+√3)=0
cosx=0      или   2sinx+√3=0
x=(π/2)+πk,k∈Z   или
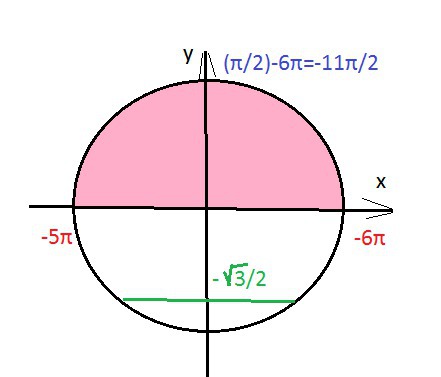
sinx=-√3/2
x=(-π/3)+2πn, n∈Z    или   х=(-2π/3)+2πm, m∈Z

x=-11π/2∈ [-6π; -5π] - корень принадлежащий отрезку.