Предмет: Геометрия,
автор: 486461kv
На сторонах АB и AD квадрата ABCD отмечены точки N и M. Точка N делит AB пополам,а точка M делит сторону AD в отношении 1:2,считая от вершины A.Определите,какую часть площади квадрата ABCD составляет прощадь треугольника ANM???
Ответы
Автор ответа:
0
см фото.
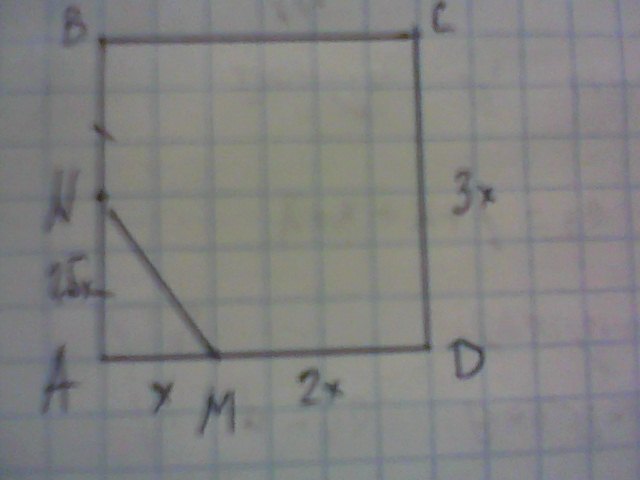
Пусть АМ=х, МD=2х, сторона квадрата АВ=3х.
Площадь квадрата равна S1=3х·3х=9х².
Площадь треугольника АNМ равна S2=0,5·1,5х·х=0,75х².
Найдем отношение площадей S1/S2=0,75х²/9х²=1/12.
Ответ: S1 составляет одну двенадцатую часть площади квадрата S2.
Пусть АМ=х, МD=2х, сторона квадрата АВ=3х.
Площадь квадрата равна S1=3х·3х=9х².
Площадь треугольника АNМ равна S2=0,5·1,5х·х=0,75х².
Найдем отношение площадей S1/S2=0,75х²/9х²=1/12.
Ответ: S1 составляет одну двенадцатую часть площади квадрата S2.
Приложения:
Автор ответа:
0
Спасибо) А почему MD =2x, если AM=1/2 AD следовательно MD=1/2 AD(тк AD= AM+MD)
Автор ответа:
0
АМ одна часть, значитх, МD 2 части. значит 2х, а вместе АD=х+2х=3х
Автор ответа:
0
Я так поступил чтобы не было дробей
Автор ответа:
0
Тогда получается, что точка М делит сторону АD в отношении 1:3, а в условии 1:2. Разве нет?
Автор ответа:
0
Ой о_о я поняла) извините пожалуйста)
Интересные вопросы
Предмет: Геометрия,
автор: SaitoUzi
Предмет: Геометрия,
автор: girlokay
Предмет: Другие предметы,
автор: Аноним
Предмет: Химия,
автор: Bigboss777