Предмет: Алгебра,
автор: Sunset234
Объясните, пожалуйста, задание. Пробовала решать сама, а ответ неверным оказался.
Докажите, что заданная функция возрастает:
Приложения:
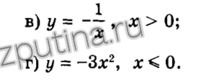
Ответы
Автор ответа:
0
Для того, чтобы решить такое задание, нужно знать и уметь пользоваться производной.
1. Найдем производную от y
y'(x) = (-1/x)' = 1/x^2
Значит y'(x) > 0 , при x>0 - функция возрастает.
2. Найдем производную от y
y'(x) = (-3x^2)' = -6x
Значит При x<=0, y'(x) >=0, значит функция возрастает
1. Найдем производную от y
y'(x) = (-1/x)' = 1/x^2
Значит y'(x) > 0 , при x>0 - функция возрастает.
2. Найдем производную от y
y'(x) = (-3x^2)' = -6x
Значит При x<=0, y'(x) >=0, значит функция возрастает
Интересные вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Геометрия,
автор: tairsv
Предмет: Литература,
автор: aleksandrabespalko74
Предмет: Биология,
автор: gurkin2004