Предмет: Геометрия, автор: lanv

В трапецию ABCD с основаниями BC и AD вписана окружность.BC=12,AD=16.Найти диаметр окружности,если CD=15.

Ответы

Автор ответа: nelle987

Если в четырёхугольник вписана окружность, то суммы длин противоположных сторон равны:
AD + BC = AB + CD

Поэтому
AB = AD + BC - CD = 16 + 12 - 15 = 13

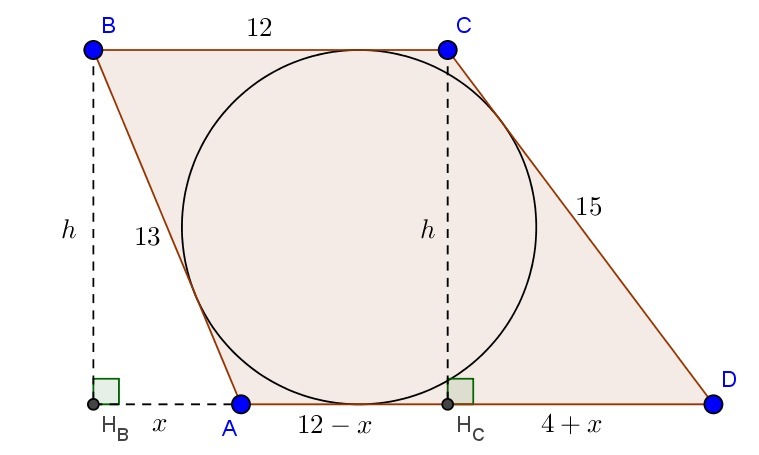
Опустим перпендикуляры из точек B и C (см. рисунок). Заметим, что так как у ABCD - трапеция и AD, BC - основания, то полученные высоты равны между собой, обозначим их длину за h. Диаметр вписанной окружности также равен h.

Пусть $AH_B = x$ . Тогда $AH_C = 12-x$ , так как $BH_BH_CC$ - по построению прямоугольник. AD = 16, поэтому $H_CD=AD-AH_C=4+x$ .

Треугольники $ABH_B$ , $CDH_C$ прямоугольные, запишем для них теорему Пифагора:
$begin{cases}13^2=h^2+x^2\15^2=h^2+(4+x)^2end{cases}$

$h^2=13^2-x^2=15^2-(4+x)^2$

Находим из последнего равенства x:
$13^2-x^2=15^2-(4+x)^2\13^2-x^2=15^2-4^2-8x-x^2\8x=15^2-13^2-4^2=40\x=5$

Итак, x = 5, тогда
$h^2=13^2-x^2=13^2-5^2=12^2\ boxed{h=12}$

Ответ. 12

Приложения: