Предмет: Геометрия,
автор: 44518
Из точки А, лежащей на окружности ,проведены две хорды АВ=8 см , АС=4√3. Найти углы треугольника АВС и радиус описанный около треугольника окружностти, если расстояние между серединами данных хорд = 2см. С рисунком пожалуйста!!! Очень надо!!!
Ответы
Автор ответа:
0
Прямая, проведённая между серединами двух сторон треугольника, называется средней линией. Она вдвое короче третьей, параллельной ей стороны, значит ВС=2·2=4 см.
По теореме косинусов cosA=(АВ²+АС²-ВС²)/(2АВ·АС)=(64+48-16)/(2·8·4√3)=√3/2 ⇒ ∠А=30°.
cosB=(АВ²+ВС²-АС²)/(2АВ·ВС)=(64+16-48)/(2·8·4)=1/2 ⇒ ∠В=60°.
∠С=180-∠А-∠В=180-30-60=90°.
В прямоугольном тр-ке, вписанном в окружность, гипотенуза является диаметром, значит радиус окружности равен её половине: R=АВ/2=8/2=4 см. - это ответ.
По теореме косинусов cosA=(АВ²+АС²-ВС²)/(2АВ·АС)=(64+48-16)/(2·8·4√3)=√3/2 ⇒ ∠А=30°.
cosB=(АВ²+ВС²-АС²)/(2АВ·ВС)=(64+16-48)/(2·8·4)=1/2 ⇒ ∠В=60°.
∠С=180-∠А-∠В=180-30-60=90°.
В прямоугольном тр-ке, вписанном в окружность, гипотенуза является диаметром, значит радиус окружности равен её половине: R=АВ/2=8/2=4 см. - это ответ.
Приложения:
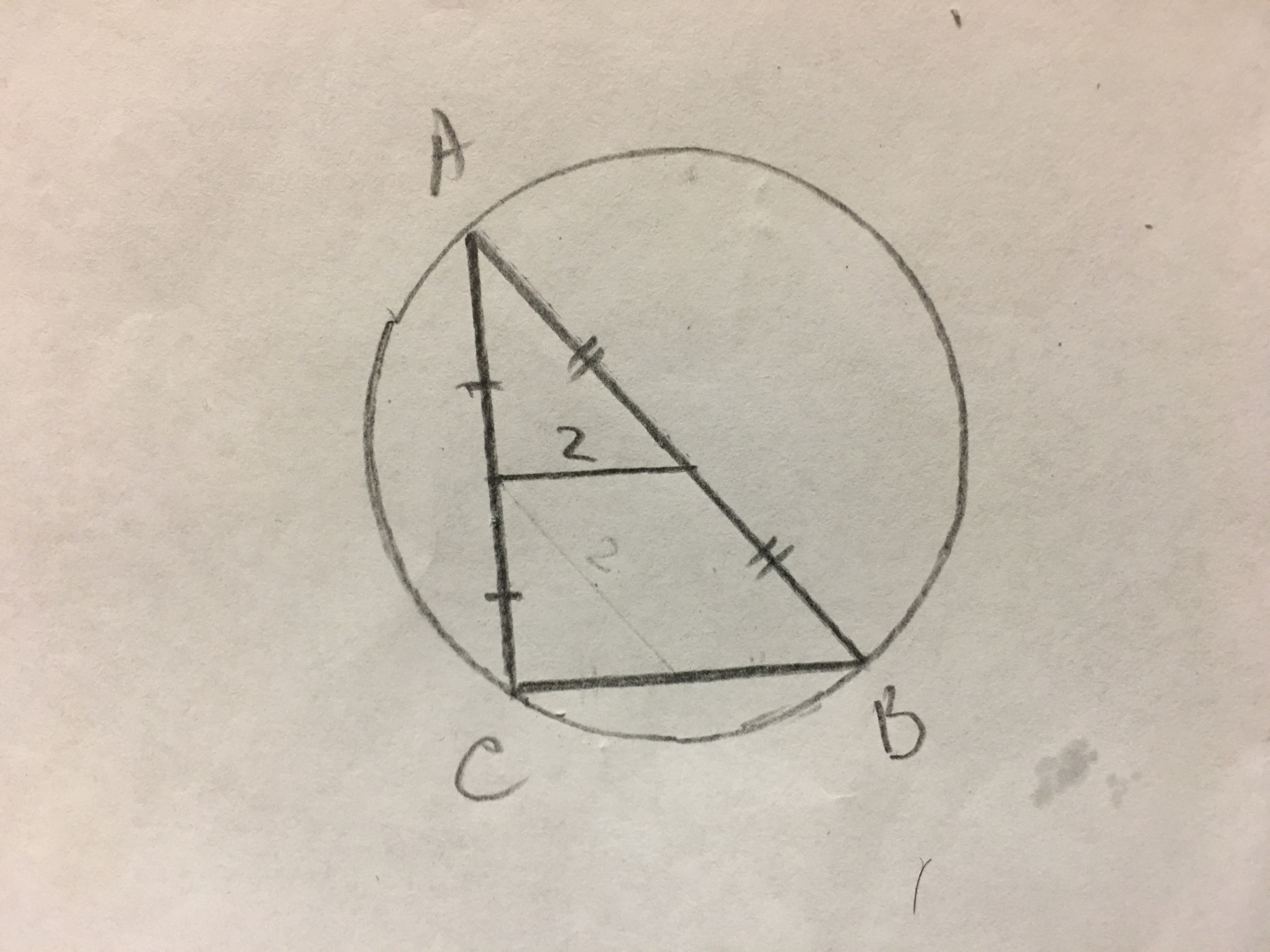
Интересные вопросы
Предмет: Химия,
автор: tileulesasem2006
Предмет: Математика,
автор: abdrakhmanova10
Предмет: Математика,
автор: klumko855
Предмет: География,
автор: oppooii
Предмет: Литература,
автор: Dimonchix