найдите интервалы возрастания и убывания функции f(x) =x^3 - x^2-x+2

Найдем производную данной функции:
f'(x)=3x²-2x-1
Найдем где производная больше нуля, а где меньше, ведь где производная больше нуля, там функция возрастает, а где меньше - убывает.
3x²-2x-1=3(x-1)(x+1/3)
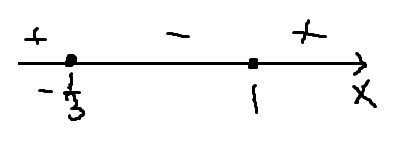
(см. вложение)
Значит, если x∈(-∞;-1/3]∪[1;+∞), то функция возрастает, если x∈(-1/3;1), то функция убывает.

спасибо большое ☺