Предмет: Алгебра, автор: dityavselennoy

Прошу, помогите пожалуйста, 8 класс

Приложения:

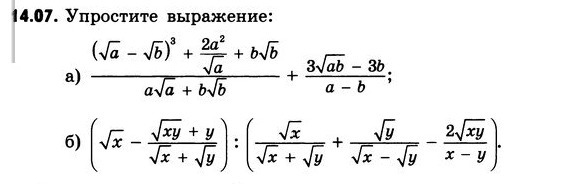
Ответы

Автор ответа: Хуqожнuк

$frac{ ( sqrt{a} - sqrt{b})^{3}+ frac{2 a^{2} }{ sqrt{a} }+b sqrt{b} }{a sqrt{a}+b sqrt{b} } + frac{3 sqrt{ab} -3b}{a-b} = \ = frac{(a sqrt{a}-3a sqrt{b}+3b sqrt{a} -b sqrt{b})+2a sqrt{a} +b sqrt{b} }{( sqrt{a} + sqrt{b} )(a- sqrt{ab}+b )} + frac{3 sqrt{b} ( sqrt{a} - sqrt{b} )}{( sqrt{a} - sqrt{b} )( sqrt{a} + sqrt{b} )} = \ = frac{3a sqrt{a} -3a sqrt{b}+3b sqrt{a}}{ sqrt{a} + sqrt{b} )(a- sqrt{ab}+b )} + frac{3 sqrt{b} }{ sqrt{a}+ sqrt{b} } =$
$= frac{3 sqrt{a}(a- sqrt{ab} +b) }{( sqrt{a} + sqrt{b} )(a- sqrt{ab}+b )} + frac{3 sqrt{b} }{ sqrt{a} + sqrt{b} } = \ = frac{3 sqrt{a}+3 sqrt{b} }{ sqrt{a} + sqrt{b} } = frac{3( sqrt{a} + sqrt{b} )}{ sqrt{a} + sqrt{b} } =3$

$( sqrt{x} - frac{ sqrt{xy}+y }{ sqrt{x} + sqrt{y} } ):( frac{ sqrt{x} }{ sqrt{x} + sqrt{y} } + frac{ sqrt{y} }{ sqrt{x} - sqrt{y} } - frac{2 sqrt{xy} }{x-y} )= \ =( sqrt{x} - frac{ sqrt{y} ( sqrt{x} + sqrt{y} )}{ sqrt{x} + sqrt{y} } ): frac{ sqrt{x} ( sqrt{x} - sqrt{y} )+ sqrt{y}( sqrt{x} + sqrt{y} )-2 sqrt{xy} }{x-y} =$
$= frac{( sqrt{x} - sqrt{y} )(x-y)}{x- sqrt{xy} + sqrt{xy}+y-2 sqrt{xy} } = \ = frac{( sqrt{x} - sqrt{y} )( sqrt{x} - sqrt{y} )( sqrt{x} + sqrt{y} )}{( sqrt{x} - sqrt{y} )^{2}} = sqrt{x} + sqrt{y}$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: SharkBreaker

мечта находит человека - это олицетворение или нет?

6 лет назад

Предмет: История, автор: Khalinasxat

1) Какова была роль жертв репрессий?
2) Роль казахской интеллигенции в обществе?
3) Кем были партизаны Великой Отечественной войны, какой героизм они совершили?

6 лет назад

Предмет: Физика, автор: deathbeach

масса корзины яблок 43 кг,определите силу тяжести действующей на Неё.
g=9,8 H/кг.
Помогите пожалуйстаа

6 лет назад

Предмет: Алгебра, автор: 19Alinka98

найдите наибольшее значение функции

у=8cos x - 27/п x+8 на отрезке [ -2п/3; 0 ]

9 лет назад

Предмет: Математика, автор: vladislavjordi

Помогите сделать номер 450

9 лет назад