Предмет: Математика,
автор: Bumla123
Три тригонометрические уравнения :22cos^2x+4sin2x=7
Ответы
Автор ответа:
0
22cos^2 x + 4sin 2x = 7
22cos^2 x + 8sin x*cos x =
= 7sin^2 x + 7cos^2 x
7sin^2 x - 8sin x*cos x -
- 15cos^2 x = 0
Делим все на cos^2 x
7tg^2 x - 8tg x - 15 = 0
(tg x + 1)(7tg x - 15) = 0
1) tg x = -1; x1=-Π/4+Π*k
2) tg x=15/7; x2=arctg(15/7)+Π*n
22cos^2 x + 8sin x*cos x =
= 7sin^2 x + 7cos^2 x
7sin^2 x - 8sin x*cos x -
- 15cos^2 x = 0
Делим все на cos^2 x
7tg^2 x - 8tg x - 15 = 0
(tg x + 1)(7tg x - 15) = 0
1) tg x = -1; x1=-Π/4+Π*k
2) tg x=15/7; x2=arctg(15/7)+Π*n
Автор ответа:
0
Ответ ответ ответ ответ ответ ответ ответ
Приложения:
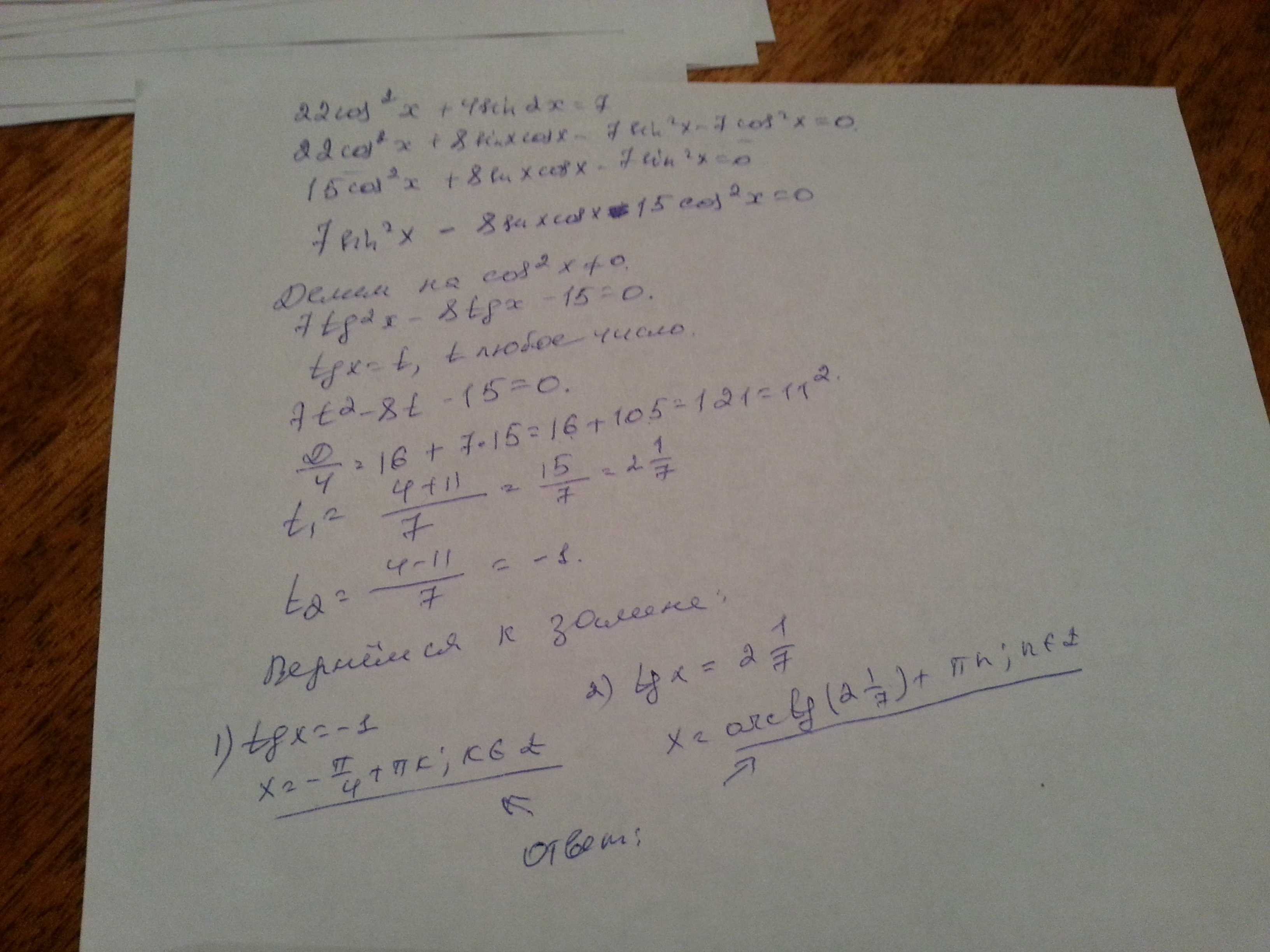
Интересные вопросы
Предмет: Математика,
автор: denisnefedev2005
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: viktoria14zt
Предмет: Математика,
автор: usip858575
Предмет: Информатика,
автор: lev23karlov