Предмет: Математика,
автор: мажд
Найти общее решение дифференциального уравнения 1-го порядка
Приложения:
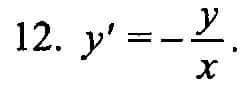
Ответы
Автор ответа:
0
y'=-y/x
dy/dx=-y/x
dy/y=-dx/x
∫dy/y=∫-dx/x
ln y = -ln x + ln C
e^(ln y) = e^(-ln x + ln C)
y=C/x, C - константа
dy/dx=-y/x
dy/y=-dx/x
∫dy/y=∫-dx/x
ln y = -ln x + ln C
e^(ln y) = e^(-ln x + ln C)
y=C/x, C - константа
Интересные вопросы
Предмет: Алгебра,
автор: dantemad53
Предмет: Информатика,
автор: bytilkavopletke4241
Предмет: Геометрия,
автор: Gavno735
Предмет: Математика,
автор: lelia59
Предмет: Биология,
автор: Илья2088