Предмет: Алгебра, автор: JM17

Помогите найти пределы

Приложения:

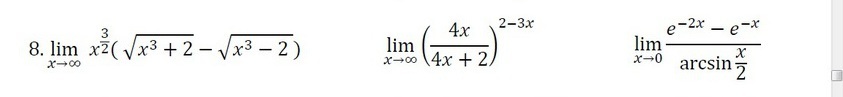
Ответы

Автор ответа: nafanya2014

1) переводим иррациональность из числителя в знаменатель:

$lim_{x to infty} frac{x^{ frac{3}{2}} cdot(x^3+2-x^3+2) }{sqrt{x^3+2}+sqrt{x^3-2}} = lim_{x to infty} frac{4x^{ frac{3}{2}} }{sqrt{x^3+2}+sqrt{x^3-2}} = frac{infty}{infty}$

Чтобы устранить неопределенность (∞/∞) делим и числитель и знаменатель на х в степени 3/2.

$lim_{x to infty} frac{4}{sqrt{1+ frac{2}{x^{ frac{3}{2} }} }+sqrt{1+ frac{2}{x^{ frac{3}{2} }} }}= frac{4}{1+1}=2$

2) Неопределенность 1^(∞). Применяем второй замечательный предел.
Выделяем целую часть из дроби 4х/(4х+2). Для этого прибавим 2 и отнимем 2 в числителе:
(4х+2-2)/(4х+2).
Делим (4х+2) на (4х+2) получаем 1 и дробь (-2/(х+2))
$lim_{x to infty} (1- frac{2}{4x+2})^{ frac{1}{ frac{-2}{4x+2} } }}=e$

Показатель степени преобразуем так.
Разделим на (-2/(4х+2)) и умножим на это же выражение.
Это выражение в знаменателе и дает е

Окончательно
$e^{ lim_{xto infty} frac{(2-3x)(-2)}{(4x+2)} }=e^{ lim_{xto infty} frac{(6x-4)}{(4x+2)} }=e^{ frac{6}{4} }=e^{ frac{3}{2} }$

3) Выносим e⁻ˣ за скобки

$= lim_{x to infty} frac{e^{-x}cdot (e^{-x}-1)}{arcsin frac{x}{2} }=$

делим числитель и знаменатель на х
О т в е т. -1/(1/2)=-2.

Автор ответа: JM17

Спасибо)

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика, автор: Аноним

вычисли:
(0,5+1/4)⋅2,1(7,4−7 1/5):2/3 = ....
(результат запиши в виде десятичной дроби).
ПОМОГИТЕ, ДАЮ 20 БАЛЛОВ!!!=)

6 лет назад

Предмет: Математика, автор: enlikenlik22

пж помогите пж пожолуйста помогите очень нужно пж помогите помогите пж пожолуйста

6 лет назад

Предмет: Русский язык, автор: asixideo