Предмет: Алгебра,
автор: chocolatexxxox
Всем доброго времени суток! :)
Не могу никак решить это выражение, помогите пожалуйста
Приложения:
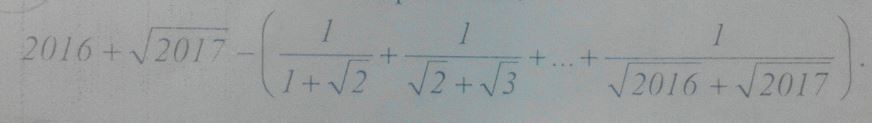
Ответы
Автор ответа:
0
Идея проста:
![frac{1}{ 1+ sqrt{2} } = frac{ sqrt{2}-1 }{(sqrt{2}+1)(sqrt{2}-1)} = frac{ sqrt{2}-1 }{2-1} =sqrt{2}-1 \ frac{1}{ sqrt{2}+ sqrt{3} } = frac{(sqrt{3}-sqrt{2})}{( sqrt{3}+ sqrt{2} )(sqrt{3}-sqrt{2})}= sqrt{3} -sqrt{2} \
frac{1}{ sqrt{3}+ sqrt{4} } = sqrt{4} - sqrt{3}
\
... \ frac{1}{sqrt{2016}+sqrt{2017}} =sqrt{2017}-sqrt{2016}](https://tex.z-dn.net/?f=+frac%7B1%7D%7B+1%2B+sqrt%7B2%7D+%7D+%3D+frac%7B+sqrt%7B2%7D-1+%7D%7B%28sqrt%7B2%7D%2B1%29%28sqrt%7B2%7D-1%29%7D+%3D+frac%7B+sqrt%7B2%7D-1+%7D%7B2-1%7D+%3Dsqrt%7B2%7D-1+%5C+frac%7B1%7D%7B+sqrt%7B2%7D%2B+sqrt%7B3%7D+%7D+%3D+frac%7B%28sqrt%7B3%7D-sqrt%7B2%7D%29%7D%7B%28+sqrt%7B3%7D%2B+sqrt%7B2%7D+%29%28sqrt%7B3%7D-sqrt%7B2%7D%29%7D%3D+sqrt%7B3%7D+-sqrt%7B2%7D+%5C+%0A+frac%7B1%7D%7B+sqrt%7B3%7D%2B+sqrt%7B4%7D++%7D+%3D+sqrt%7B4%7D+-+sqrt%7B3%7D+%0A%5C%0A++...+%5C+frac%7B1%7D%7Bsqrt%7B2016%7D%2Bsqrt%7B2017%7D%7D+%3Dsqrt%7B2017%7D-sqrt%7B2016%7D "frac{1}{ 1+ sqrt{2} } = frac{ sqrt{2}-1 }{(sqrt{2}+1)(sqrt{2}-1)} = frac{ sqrt{2}-1 }{2-1} =sqrt{2}-1 \ frac{1}{ sqrt{2}+ sqrt{3} } = frac{(sqrt{3}-sqrt{2})}{( sqrt{3}+ sqrt{2} )(sqrt{3}-sqrt{2})}= sqrt{3} -sqrt{2} \
frac{1}{ sqrt{3}+ sqrt{4} } = sqrt{4} - sqrt{3}
\
... \ frac{1}{sqrt{2016}+sqrt{2017}} =sqrt{2017}-sqrt{2016}")
Теперь ясно что в большой скобке сократится все кроме √(2017)-1
Тогда значение выражения равно
2016+√(2017)-(√(2017)-1)=2017
Теперь ясно что в большой скобке сократится все кроме √(2017)-1
Тогда значение выражения равно
2016+√(2017)-(√(2017)-1)=2017
Интересные вопросы
Предмет: Окружающий мир,
автор: irinakurilova4353
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: vladzabolotnij0
Предмет: Математика,
автор: yusovavika
Предмет: Биология,
автор: abybakarowa