Предмет: Геометрия,
автор: Диантус
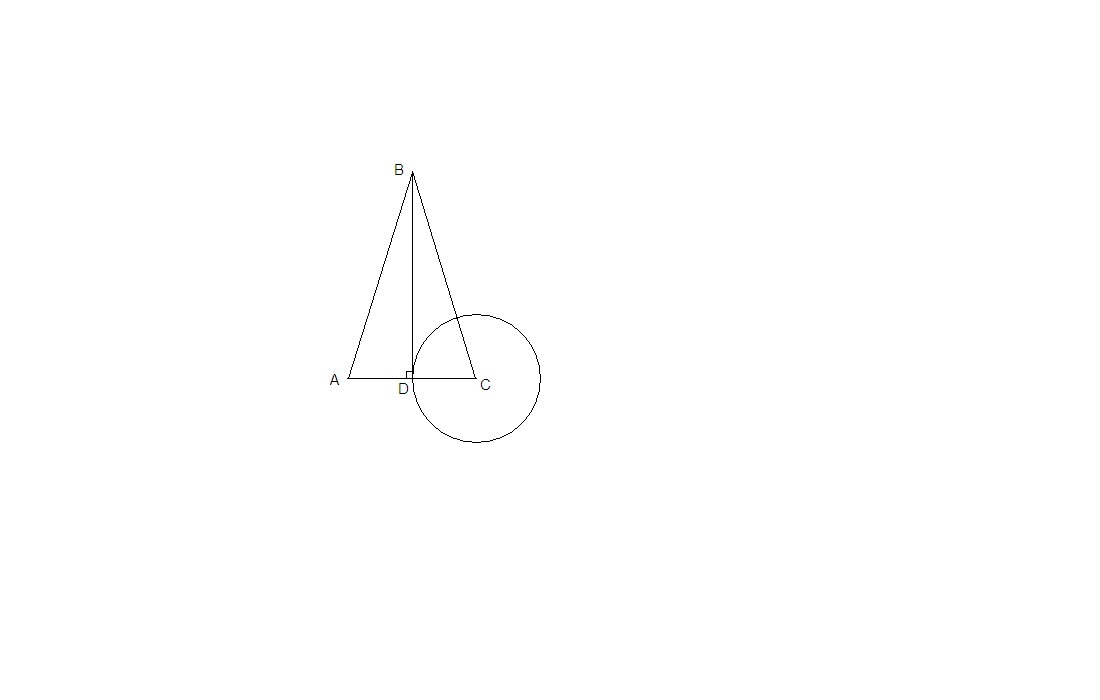
В равнобедренном треугольнике ABC c основанием AC проведена медиана BD.Докажите,что прямая BD касается окружности с центром C и радиусом,равным AD
Ответы
Автор ответа:
0
BD - медиана равнобедренного треугольника, проведенная к основания, значит и высота.
R = AD = CD.
Значит, CD⊥BD. CD - расстояние от центра окружности до прямой BD.
И CD - радиус окружности.
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая является касательной.
Значит BD - касательная к окружности с центром С и радиусом CD.
Доказано
R = AD = CD.
Значит, CD⊥BD. CD - расстояние от центра окружности до прямой BD.
И CD - радиус окружности.
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая является касательной.
Значит BD - касательная к окружности с центром С и радиусом CD.
Доказано
Приложения:
Интересные вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Литература,
автор: firi534t
Предмет: Математика,
автор: zanajymberikbol
Предмет: Физика,
автор: Платинум
Предмет: Алгебра,
автор: Camagum