Предмет: Алгебра, автор: safiullova13

решите уравнения пожалуйста!!! ПРОШУ

Приложения:

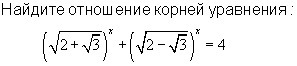
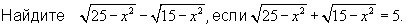
Ответы

Автор ответа: NNNLLL54

$1); ; (sqrt{2+sqrt3})^{x}+(sqrt{2-sqrt3})^{x}=4\\\sqrt{2+sqrt3}= frac{sqrt{2+sqrt3}cdot sqrt{2-sqrt3}}{sqrt{2-sqrt3}}=frac{sqrt{4-3}}{sqrt{2-sqrt3}}= frac{1}{sqrt{2-sqrt3}}\\\t=(sqrt{2+sqrt3})^{x}; ; to ; ; (sqrt{2-sqrt3})^{x}=frac{1}{t}; ,; ; t textgreater 0\\t+frac{1}{t}=4\\frac{t^2-4t+1}{t}=0; ; to ; ; t^2-4t+1=0; ,; tne 0\\(t-2)^2-4+1=0\\(t-2)^2=3; ; to ; ; t-2=pm sqrt3; ,; ; t=2pm sqrt3\\a); ; (sqrt{2+sqrt3})^{x}=2+sqrt3$

$(2+sqrt3)^{frac{x}{2}}=2+sqrt3\\frac{x}{2}=1; ; to ; ; x=2\\b); ; (sqrt{2+sqrt3})^{x}=2-sqrt3; ,; ; ; ; ; ; 2-sqrt3=frac{1}{2+sqrt3}\\(sqrt{2+sqrt3})^{x}=frac{1}{2+sqrt3}; ; to ; ; (sqrt{2+sqrt3})^{x}=(2+sqrt3)^{-1}\\(2+sqrt3)^{frac{x}{2}}=(2+sqrt3)^{-1}\\frac{x}{2}=-1; ; to ; ; x=-2\\Otvet:; ; x=-2,; ; x=2; .$

$2)quad sqrt{25-x^2}+sqrt{15-x^2}=5\\sqrt{25-x^2}-sqrt{15-x^2}= frac{(sqrt{25-x^2}-sqrt{15-x^2})(sqrt{25-x^2}+sqrt{15-x^2})}{sqrt{25-x^2}+sqrt{15-x^2}} =\\= frac{(25-x^2)-(15-x^2)}{5} = frac{10}{5}=2$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Английский язык, автор: fenukivanka

Говоріня на тему "Подорож" допоможіть будь ласка

6 лет назад

Предмет: Геометрия, автор: nelkindevilborn

Постройте график функции y=3-2x-2x^2 Найдите:
а) область значений функции;
б) при каких значениях аргумента функция возрастает.

6 лет назад

Предмет: Геометрия, автор: ssevcenko694

одна из сторон параллелограмма равна 14см. Найдите другую сторону параллелограмма если его периметр равен 36см

6 лет назад

Предмет: Математика, автор: Марияма

Запишите дроби в порядке возрастания 1/2, 17/20, 2/5, 3/4

9 лет назад

Предмет: Математика, автор: bolatyes

Задание номер 4. Сравни :

9 лет назад