Предмет: Геометрия,
автор: vlad1bavrin
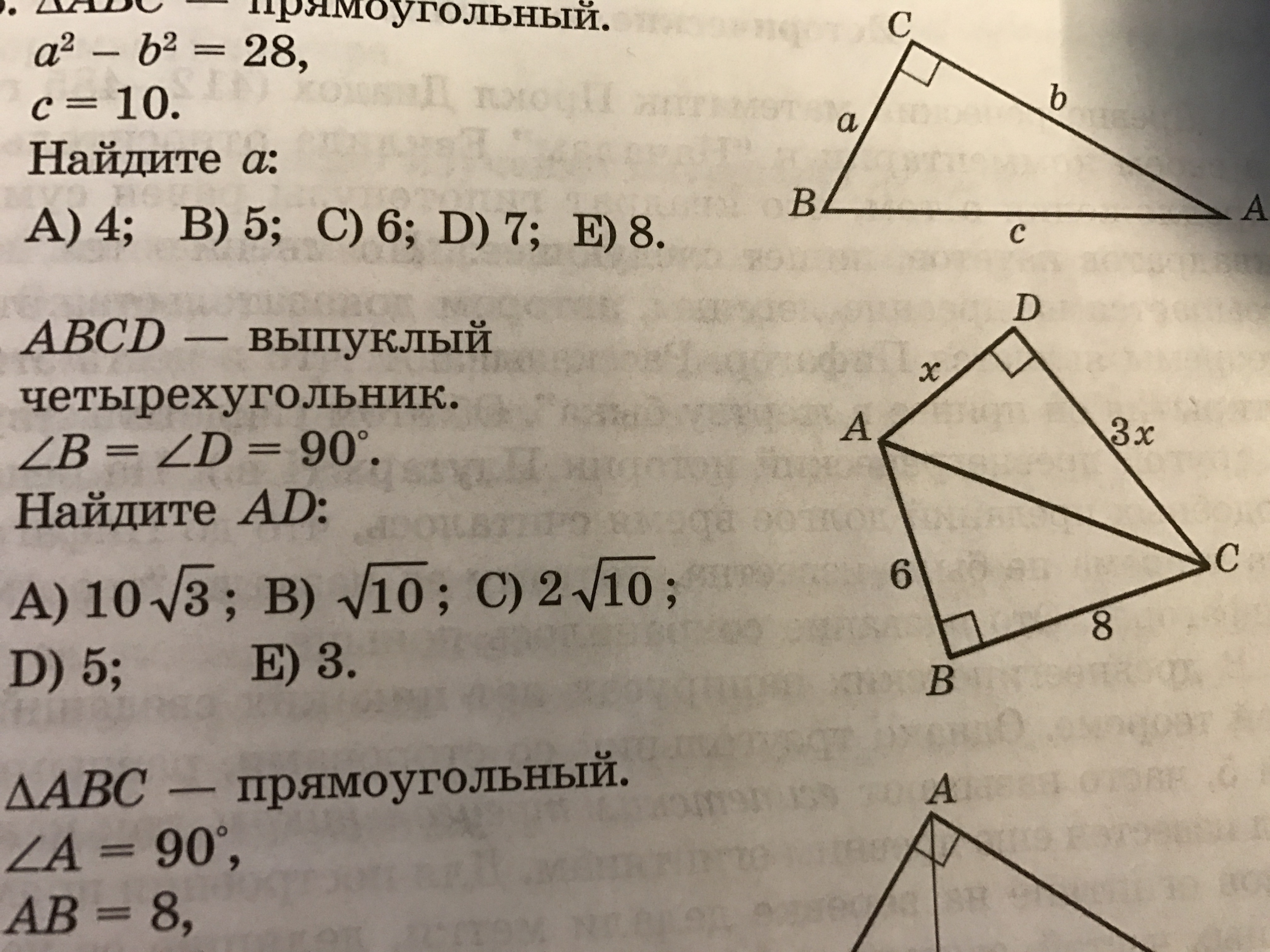
Дано:АВСD-выпуклый четырехугольник.Угол В=углу D=90 градусов.
Найдите AD.
Приложения:
Ответы
Автор ответа:
0
Четырехугольник АВСD диагональю АС поделен на два прямоугольных треугольника, в одном из которых известны катеты. АС - общая гипотенуза.
В ∆ АВС отношение катетов 6:9=3:4, что указывает на то, что ∆ АВС - египетский. АС=10 ( проверьте по т.Пифагора).
Из второго треугольника:
АС=√(АD²+DC²) 100=√(х²+9х²)
10х²=100
х²=10, х=√10 - Верным является вариант В.
Интересные вопросы
Предмет: История,
автор: bbnzjayayywhwh
Предмет: Українська мова,
автор: Taelknow
Предмет: Биология,
автор: 45455557777777
Предмет: Математика,
автор: Berezgova