Предмет: Математика, автор: Аноним

Помогите вычислить интегралы очень вас прошу, застряла на этих примерах

Приложения:

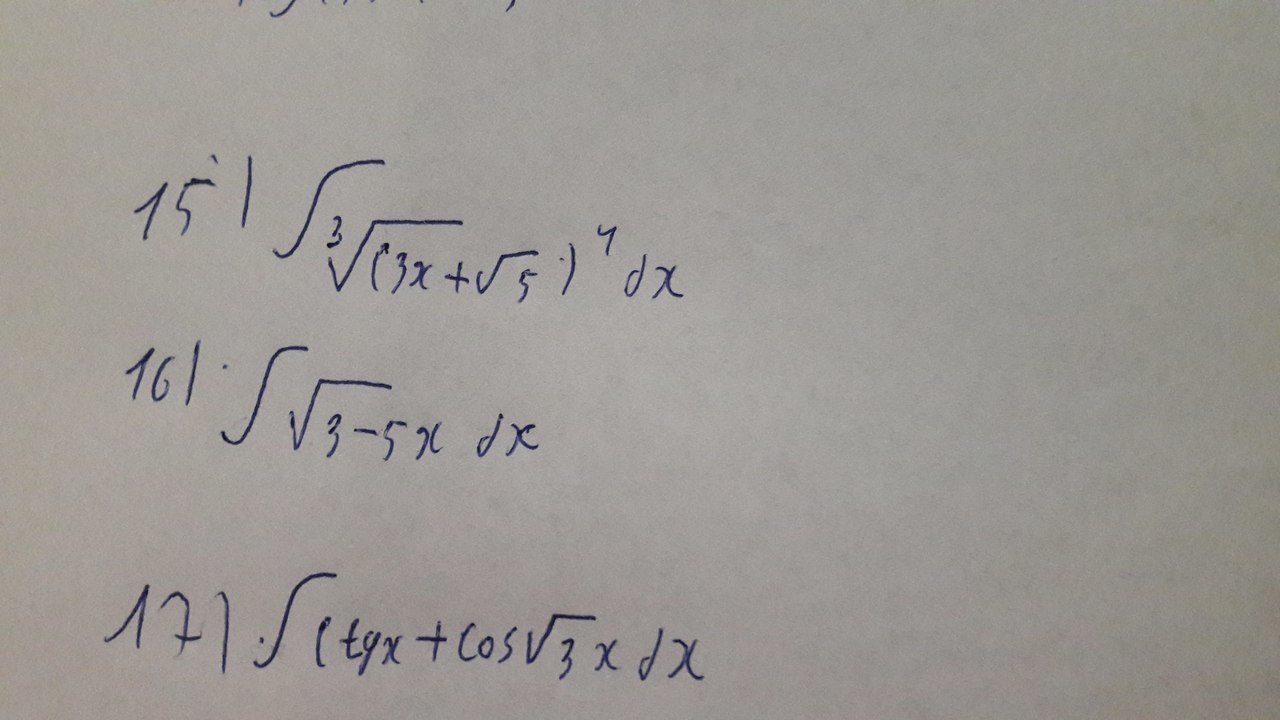
Ответы

Автор ответа: sedinalana

15
$intlimits { sqrt[3]{(3x+ sqrt{5})^4 } } , dx =3/7* sqrt[3]{(3x+ sqrt{5} )^7} *1/3+C=$ $1/7* sqrt[3]{(3x+ sqrt{5} )^7} +C$
16
∫√(3-5x)dx=2/3*√(3-5x)³ *(-1/5)+C=-2/15*√(3-5x)³+C
17
$intlimits {(tgx+cos sqrt{3} x)} , dx = intlimits {tgx} , dx + intlimits {cos sqrt{3} x} , dx =-ln(cos x)+1/ sqrt{3} *$ $sin sqrt{3} x+C$
-----------------------------------
∫tgxdx=∫(sinx/cosx)dx=-∫dt/t=-lnt=-ln(cosx)
t=cosx,dt=-sinxdx
∫cos√3x=1/√3*sin√3x

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Алгебра, автор: Аноним

ДАЮ 30 БАЛОВ Помогите срочно!!!!!!!!!! как решить уравнение и записать ответ в виде десятичной дроби
3x(x-7)-x(4+3x)=5

6 лет назад

Предмет: Математика, автор: hristinanolikova

помогите пожалуйста 6 клас!

6 лет назад

Предмет: Қазақ тiлi, автор: katyakot0372

1.Реттік сандарды тап.
А. екеу ,төртеу, бесеу
В. бір, екі, үш
С. бірден, үштен, оннан
D. бесінші, оныншы, он үшінші
Е. екіден бір, сегізден үш, бестен екі
2. Жалқы есім бар сөйлем
А.Әкесімен бірге бақшаны аралады.
В.Мен теледидар көргенді ұнатамын
С.Үнемі әлем жаңалықтарын қараймын
D.Кеше Алматы қаласында кездесу өткіздік
E.Спорт арнасын үзбей қараймын
3. Жалпылау есімдігі қатысқан сөйлем
А.Күллі халық әдет-салты түлетуде
В.Күн сәулесі нұрын шашады
С.Мен мұны әнмен оятайын
D.Менің сендерге айтайын өсиет бар
E.Біз бәсеге қабілетті елміз
4.Мезгіл үстеу кездесетін қатар
А . Таңертең тұрады
В. Тауға қарай өрмелеу
С. Алға жылжыды
D. Әрен келеді
Е. Ақырын жүреді
5. Дұрыс жазылған сөздер қатары
А. Құлұн, белбеу, сексен
В. хат, сембе, хал
С. сексен, тоқсан, өрүк
D. Қыстыгүні, сембе, хабар
Е. хат, хабар, белбеу
6.Синоним бар сөйлем
А . Адамның алғашқы қалыптасуы отбасынан басталады
В. Адам бойындағы алғашқы адамгершілік белгілер отбасында қалыптасады.
С. Отбасы-сыйластық ,жарастық орнаған орта.
D. Баланың тәрбиелі болып өсуіне берекелі отбасының әсері мол.
Е. Тәрбие отбасынан басталады
7.Сілтеу есімдігі орналасқан қатар
А.мен,сен,сіз,ол
В.кім не неше
С.біреу,кейбір,
D.бұл,осы,сол,анау.
E.ешкім,ешбір,мынау
8. Шылаулар – ол......
А. местоимение
В. наречие
С. причастие
D. союзы
Е. междометие
9. Көптік жалғауы жалғанған сөзді табыңдар.
А. қатар
В. көтер
С. жолдар
D. болар
Е. қодар
10. Сын есімді көрсетіңіз.
А. қызыл, көк, кең
В.кітап, көмір, қар
С. қырық, елу, алпыс
D. қанша, қалай, кім
Е. қарайды, күтеді, келеді
11. Заттың түрін, түсін, сапасын білдіретін сөз табы.
А. зат есім
В.сын есім
С. сан есім
D. етістік
Е. Есімдік
12. Есім сөзден сын есім жасайтын жұрнақтар
А. –ғыр,-гір, -қыр, -кір
В. – лы, -лі, -ды, -ді
С. – інші, -нші, -ыншы, -ншы
D. –лық, -лік, -дық, -дік
Е. – лау, - леу, -дау, -деу
13. Есімшенің жұрнақтарын белгілеңіз
А. –ған,-ген, -қан, -кен
В. – ар, -ер, -р, -с
С. – інші, -нші, -ыншы, -ншы
D. –лық, -лік, -дық, -дік
Е. – лау, - леу, -дау, -деу
14.Жалғаулық шылау мағынасына қарай неше топқа бөлінеді
А. 2
В. 3
С. 5
D. 6
Е. 7
15. Қарсылықты жалғаулықтарды анықта
А. мен, және, да
В. не, әлдене, кейде
С. өйткені, сол себепті, сол үшін
D. егер, онда, әйтпесе
Е. бірақ, алайда, дегенмен
16. Қатаң дауыссызды көрсетіңіз.
А. д, в, с
В. б, й, р
С. п, ш, қ
Д. м, ң, н
Е. ғ, л, у
17. Тәуелдік жалғауы бар зат есімді табыңыз.
А. Басқа
В. Аяғым
С. Кеудеден
Д.Қолдың
Е. Көзді
18. Жіктеу есімдігін табыңыз.
а. бұлар
ә. қайдан
б. олар
в. кейбіреу
г. ешкім
19. Зат есім қандай сұрақтарға жауап береді ?
А.қашан?
В. кім ? не ?
С. қандай ?
D. не істейді ?
Е. нешеу ?
20. Заттың атын білдіретін сөздерді не деп атайды?
А. етістік
В. үстеу
С. есімдік
D. сын есім
Е. зат есім

6 лет назад

Предмет: Физика, автор: njudina75

чтобы измерить диаметр проволоки ее намотали вплотную на карандаш сделав 30 витиков определите диамерт проволоки

9 лет назад

Предмет: История, автор: аня326

фашизм в италии в политической сфере

9 лет назад