Найти площадь криволинейной трапеции, ограниченной следующими графиками:
y = 2x; y = x^2.
Желательно с подробным решением. Заранее спасибо.

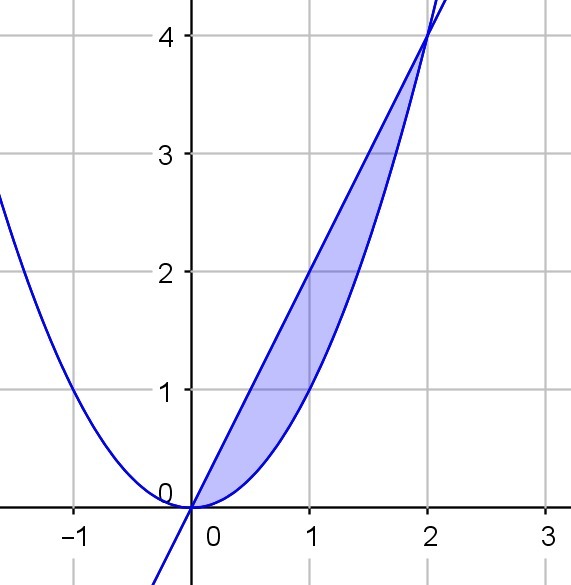
Область имеет вид, изображённый на рисунке. Точки пересечения графиков находим из решения системы
{y = 2x, y = x^2}
(x, y) = (0, 0) или (2, 4)

Площадь подграфика равна определённому интегралу от функции, площадь такой криволинейной трапеции - от разности функций.



Ответ.  S = 4/3