найдите наименьшее значение функции y=x в квадрате+441/x на отрезке[2;32]

нужно найтим произыодную от это функции по формуле:  

(fg)'= f'g - fg'g^2

применяем,получается

y'= x^2 - 441 x^2

приравниваем вс к нулю

x^2 - 441 = 0          x^2  НЕ РАВНО 0

x^2=441

x=+-21  т.к  -21 не принадлжеит отрезку [2;32]

подставляем 21,2 и 32 в изначальную функцию.

x=21

y=42

x=2

y=222,5

х=32

у= 45,78......

нужно найти наименьший

Ответ:42

ОДЗ: x≠0.

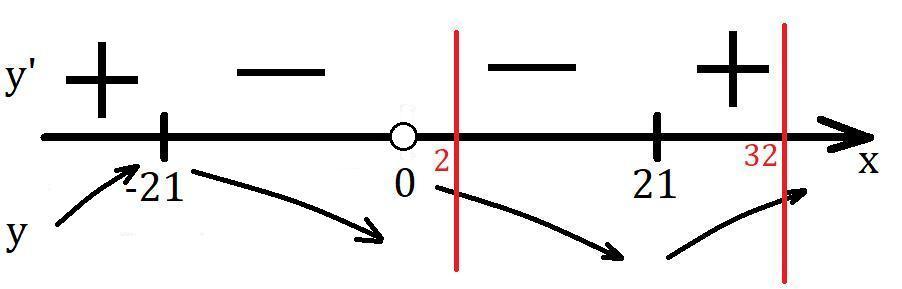
Делаем схематический рисунок, смотри в приложении.

При x∈[2;21] функция убывает; при х∈[21;32] функция возрастает. Поэтому наименьшее значение будет при х=21.

Ответ: 42.