диаметр шара равен высоте цилиндра осевое сечение которого есть квадрат. найдите отношение объемов шара и цилиндра

Объём шара считается по формуле:

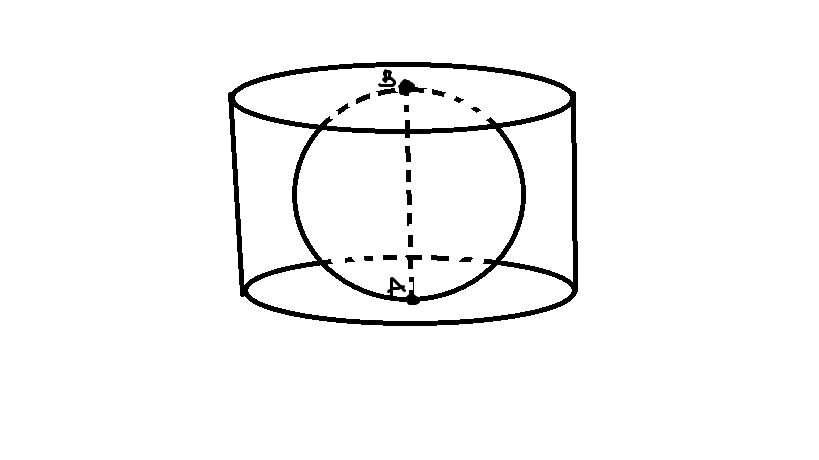
На рисунке видно AB - диаметр шара и высота цилиндра.

Пусть - радиус шара. Тогда объём шара равен:

Объём цилиндра:

Где r - радиус основания цилиндра, h- высота цилиндра. 

Высота цилиндра вдвое больше радиуса(т.к. высота есть диаметр круга(по условию))=

Т.к. Осевым сечением цилиндра является квадрат, то половина высоты цилиндра будет равна радиусу основания цилинадра. Тоесть

Теперь объём цилиндра: