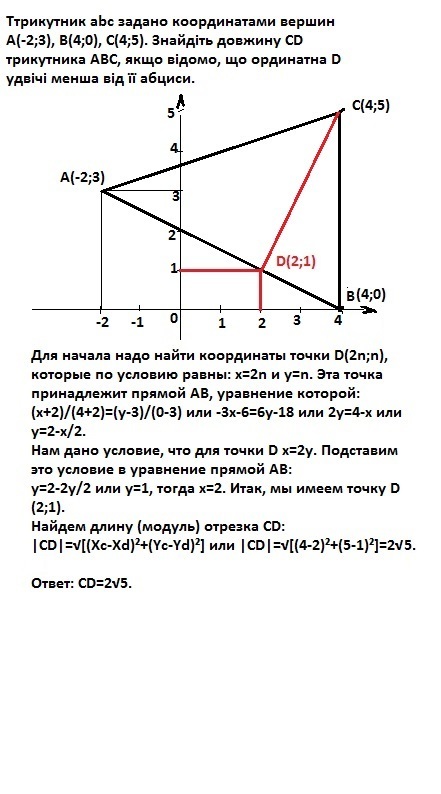
трикутник abc задано координатами вершин A(-2;3), B(4;0), C(4;5). Знайдіть довжину CD трикутника ABC, якщо відомо, що ординатна D удвічі бменша від її абциси

Для начала надо найти координаты точки D(2n;n), которые по условию равны: х=2n и y=n. Эта точка принадлежит прямой АВ, уравнение которой:
(x+2)/(4+2)=(y-3)/(0-3) или -3x-6=6y-18 или 2y=4-x или y=2-x/2.
Нам дано условие, что для точки D координата x=2y.
Подставим это условие в уравнение прямой АВ:
y=2-2y/2 или y=1, тогда х=2. Итак, мы имеем точку D(2;1).
Найдем длину (модуль) отрезка СD:
|CD|=√[(Xc-Xd)²+(Yc-Yd)²] или |CD|=√[(4-2)²+(5-1)²]=2√5.
Ответ: СD=2√5.