Предмет: Алгебра, автор: mocor

Помогите решить неравенство, с подробным решением, пожалуйста, срочно! (
Если что, в начале тройка

Приложения:

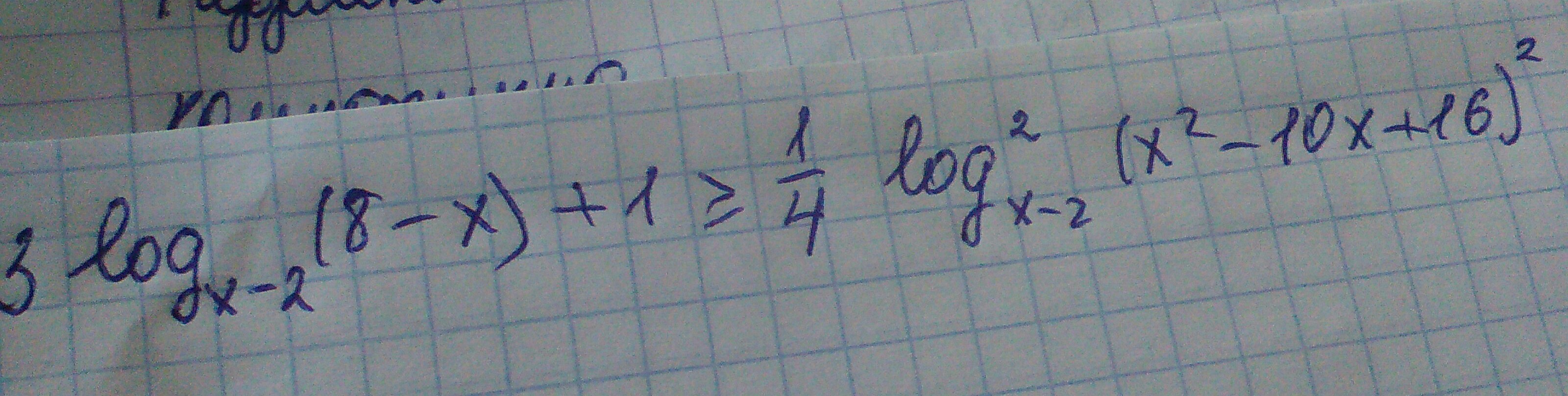
Ответы

Автор ответа: nelle987

$3log_{x-2}(8-x)+1geqslantdfrac14log_{x-2}^2(x^2-10x+16)^2\ 3log_{x-2}(8-x)+1geqslantdfrac14log^2_{x-2}((x-8)(x-2))^2\ 3log_{x-2}(8-x)+1geqslantdfrac14(log_{x-2}(x-8)^2+log_{x-2}(x-2)^2)\ 3log_{x-2}(8-x)+1geqslantdfrac14(2log_{x-2}(8-x)+2)^2\ 3log_{x-2}(8-x)+1geqslantlog^2_{x-2}(8-x)+2log_{x-2}(8-x)+1\ log_{x-2}^2(8-x)-log_{x-2}(8-x)leqslant0\ log_{x-2}(8-x)(log_{x-2}(8-x)-1)leqslant 0$

Теперь воспользуемся теоремой о знаке логарифма, оно же метод рационализации, ....
Суть метода: если логарифмы определены, то $log_{f(x)}g(x)-log_{f(x)}h(x)$ даёт такой же знак, что и $(f(x)-1)(g(x)-h(x))$ .

ОДЗ: x - 2 > 0, x - 2 ≠ 1, 8 - x > 0
x ∈ (2, 3) ∪ (3, 8)

На ОДЗ неравенство равносильно такому:
$(x-3)^2(8-x-1)(8-x-(x-2))leqslant 0\ (x-3)^2(7-x)(10-2x)leqslant0\(x-3)^2(x-5)(x-7)leqslant0$

Получилось обычное равенство, которое легко решается методов интервалов:
$xin{3}cup[5,7]$

Это решение, кроме 3, входит в ОДЗ, поэтому окончательный ответ такой:
$boxed{xin[5,7]}$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика, автор: neckrichdiana

срочнооо!!!! тут нужно ответить на 2 вопроса
Учень прочитав 30 сторінок книжки, яка містить 60 сторінок.Яку частину книжки(у відсотках) він прочитав?/ и второе
Учень прочитав 60% усієї книжки, яка містить 30 сторінок. Скільки сторінок йому залишилося прочитати? прошу помогитееее

6 лет назад

Предмет: Математика, автор: ytmarlenayt

60. Отметьте в тетради точку О. Постройте две окружности с центром в этой точке: одну радиусом 2 см, другую радиусом 3 см. За- красьте цветным карандашом область, рас- положенную между этими окружностями. Как бы вы назвали получившуюся фигуру?

6 лет назад

Предмет: Музыка, автор: MELEKLER87

Способна ли музыка сотворить чудо остновить зло?

6 лет назад