Предмет: Алгебра,
автор: Skalozub
решите уравнение 4sin^2 x=3
Ответы
Автор ответа:
0
4sin^2 x=3
sin^2 x=3/4
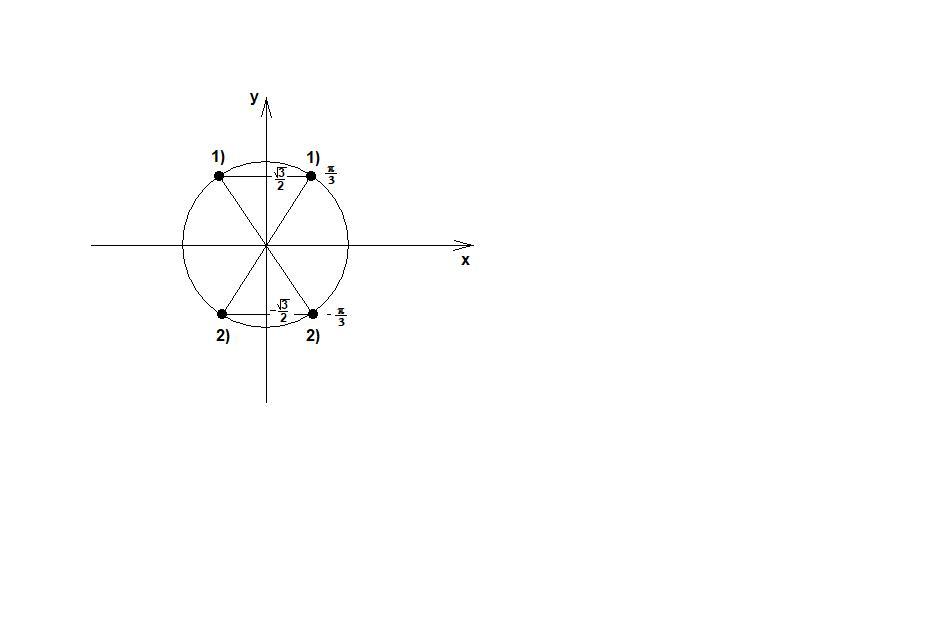
sinx=sqrt(3)/2 (1) или sinx=-sqrt(3)/2 (2)
1)
x=П/3+2Пk , k пренадл. Z или x=2П/3+2Пk , k пренадл. Z
2)
x=-П/3+2Пk , k пренадл. Z или x=-2П/3+2Пk , k пренадл. Z
Ответ:{П/3+Пk/2 | k пренадл. Z}
Автор ответа:
0
Ответ:
x = ± π/3 + πn, n∈Z
Объяснение:
4sin²x = 3
sin²x = 3/4
sinx = ± √3/2
1) sinx = √3/2
x = (- 1)ⁿ · arcsin (√3/2) + πn, n∈Z
x = (- 1)ⁿ · π/3 + πn, n∈Z
2) sinx = - √3/2
x = (- 1)ⁿ · arcsin (- √3/2) + πn, n∈Z
x = (- 1)ⁿ⁺¹ · arcsin (√3/2) + πn, n∈Z
x = (- 1)ⁿ⁺¹ · π/3 + πn, n∈Z
Корни можно объединить:
x = ± π/3 + πn, n∈Z
Приложения:
Интересные вопросы
Предмет: Химия,
автор: dashaniko96
Предмет: Қазақ тiлi,
автор: nkairbekova7
Предмет: Литература,
автор: valeriabirukova04
Предмет: Математика,
автор: monster1223
Предмет: Химия,
автор: lenochka9000