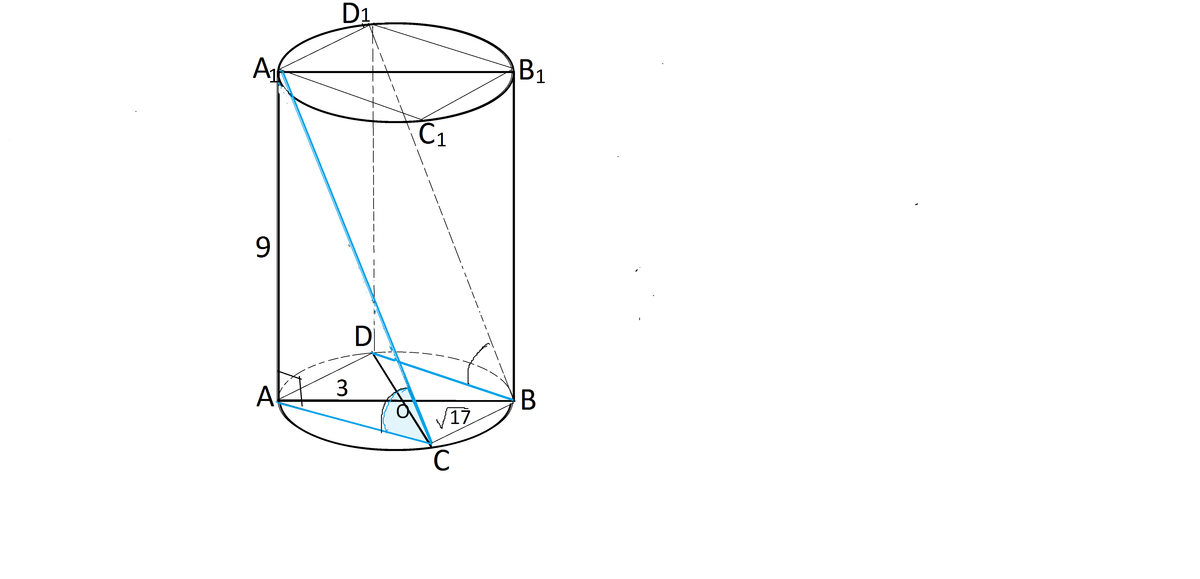
Радиус основания цилиндра равен 3, а высота равна 9. Отрезки AB и CD диаметры одного из оснований цилиндра, а отрезки AA1 его образующая . Известно, что BC=корень из 17. Найдите синус угла между прямыми A1C и BD.

Так как оба отрезка - диаметры, треугольник АВС - прямоугольный.

АВ в нем - гипотенуза, АС и ВС - катеты.

АС²=АВ²-ВС²=36-17=19

АС=√19

Соединим D1 с В.

A1D1=AD=CB

AC=DB

A1D1BC - параллелограмм

АА1=DD1

D1B=A1C

Угол между прямыми A1C и BD равен углу D1BD между D1B и DB

Угол А1СА=D1BD

Синус А1СА= А1А:А1С

А1С²= А1А²+АС²=81+19=100

А1С=√100=10

sin A1CA=9:10=0,9