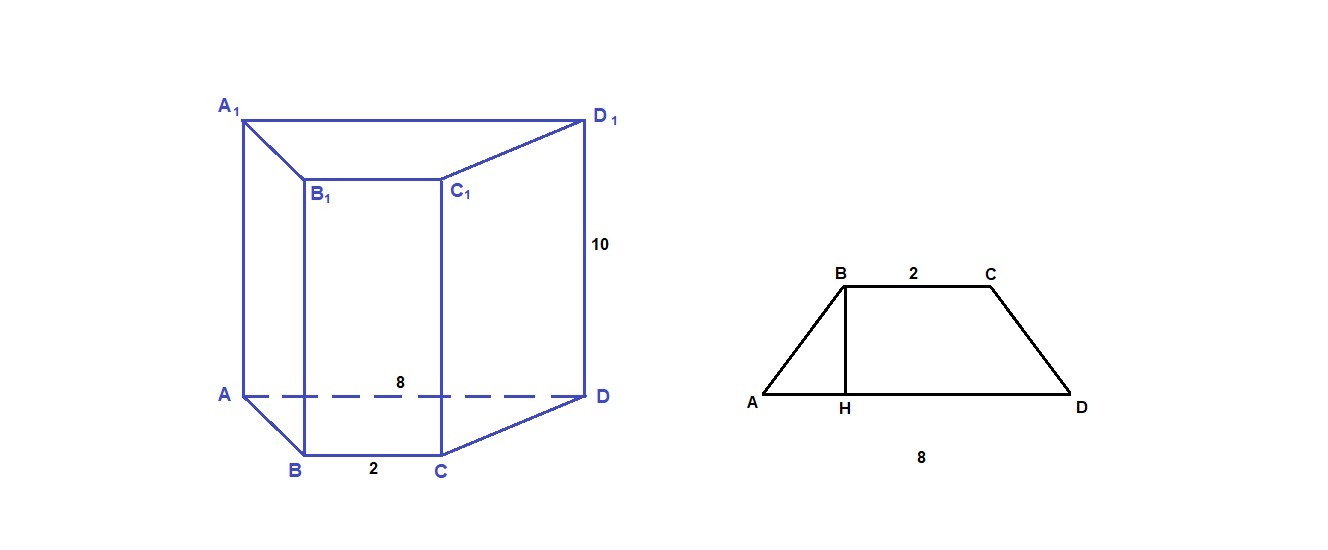
1 . Боковое ребро прямой призмы равно 10 см , а ее объем - 200 см3 . Основание призмы - равнобокая трапеция с основаниями 2 и 8 см . Найдите полную поверхность призмы

Объем призмы:

V = Sосн · AA₁

200 = Sосн · 10

Sосн = 200/10 = 20 см²

Sосн = (AD + BC)/2 · BH

20 = (8 + 2)/2 · BH

20 = 5 · BH

BH = 4 см

Высота в равнобедренной трапеции делит большее основание на отрезки, один из которых равен полусумме оснований (больший), а другой - полуразности оснований.

АН = (AD - BC)/2 = (8 - 2)/2 = 3 см

ΔАВН - прямоугольный, египетский, значит АВ = 5 см

Sполн = Sбок + 2Sосн

Sбок = Росн · АА₁ = (8 + 2 + 5 · 2) · 10 = 200 см²

Sполн = 200 + 2 · 20 = 240 см²