Предмет: Математика, автор: 1368165491034asdfg

Вычислить площадь фигуры, ограниченной линиями y=- $frac{2}{9}$ $x^{3}$ + $frac{4}{3}x;$ ; y=0.

Ответы

Автор ответа: vadim899

0

x*(-2/9x^2+4/3)

x=0 x^2=6

x=+-корень из 6

F(x)=-x^4/18+2x^2/3 итеграл от -корня из 6 до корня из 6

12+4+12-4=24

У меня вот так получилось конечно могу и ошибаться...

Удачи ;)

Автор ответа: hELFire

0

$y=-frac{2}{9}x^3+frac{4}{3}x=-frac{2}{9}x(x^2-6)$

корни уравнения

$x in {-sqrt{6}, 0, sqrt{6}}$

Площадь фигуры:

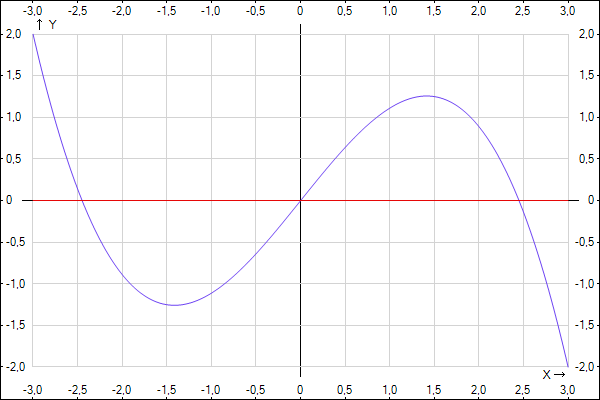
$S = int_{-sqrt{6}}^0(frac{2}{9}x^3-frac{4}{3}x)dx + int_0^{-sqrt{6}}(-frac{2}{9}x^3+frac{4}{3}x)dx=\ =(frac{2}{36}x^4-frac{4}{6}x^2)|_{-sqrt{6}}^0+(-frac{2}{36}x^4+frac{4}{6}x^2)|_0^{sqrt{6}}=\ =-frac{1}{18}*36 +frac{2}{3}*6- frac{1}{18}*36 +frac{2}{3}*6= 4$

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Алгебра, автор: aloshina20

Показник степеня дорівнює (с4)3

6 лет назад

Предмет: Қазақ тiлi, автор: serikegizekov

1.Фонетика зерттейтін саланы белгілеңіз.

A) Сөз құрамы
B) Сөйлем мүшелері
C) Дыбыстар жүйесі
Д) Сөз таптары
E) Сөз мағынасы

6 лет назад

Предмет: Математика, автор: Snezhinka666

Если все рабочие за 5 дней делают 1287 деталей а один 143 деталей то 1. Сколько всего рабочих? 2. Сколько все рабочие сделают деталей за неделю?

6 лет назад

Предмет: Литература, автор: LOLMASTER

О чём сожалеет поэт и что его радует? в стихотворении "Бородино"

10 лет назад

Предмет: Обществознание, автор: Маняша1

Немецкий философ И. Кант написал:" Дисциплина- это средство уничтожить в человеке его дикость". Как ты думаешь, какой смысл вложены слово " дикость"? В чем помогает человеку дисциплина?

10 лет назад