Предмет: Алгебра, автор: ПомаГайка

Обчислити(там кубический корень, плоховато видно (: )

корень кубический из (8 + 3 корня из 21) + корень кубический из (8 - 3 корня из 21)

Приложения:

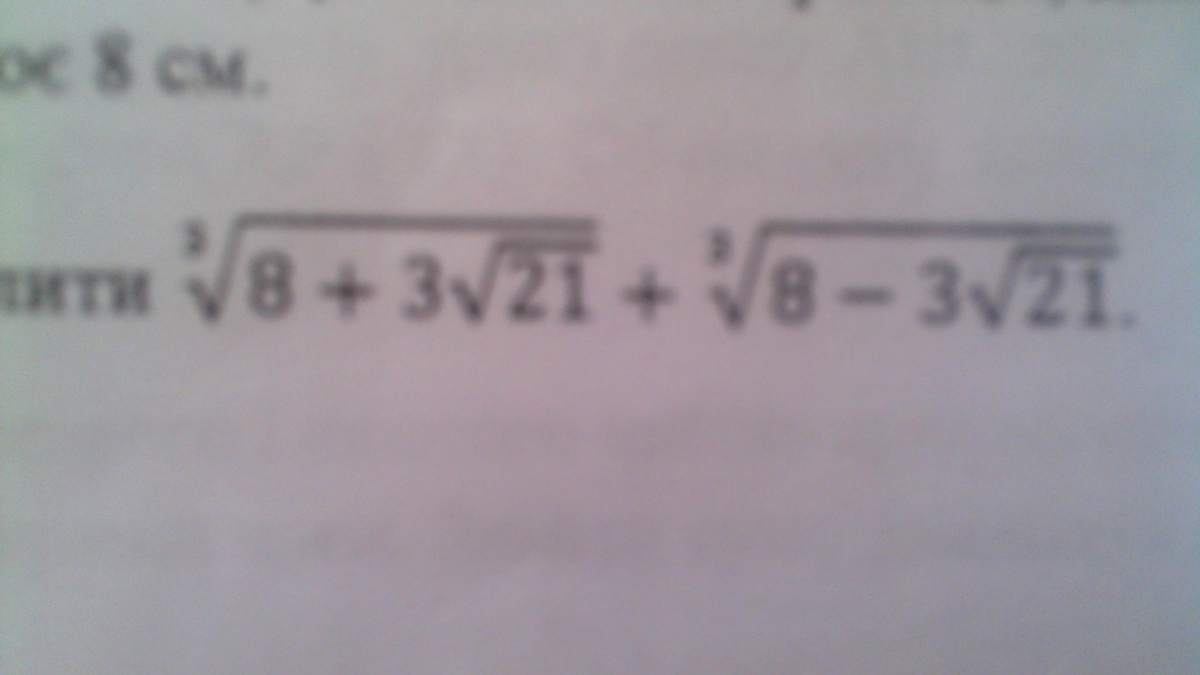
Ответы

Автор ответа: dtnth

0

Обозначим $A=sqrt[3]{8-3sqrt{21}}+sqrt[3]{8+3sqrt{21}}$ , заметим, что число А - дейсвительное число

тогда по формуле куба суммы двучлена $(a+b)^3=a^3+b^3+3ab(a+b)$

свойству корня $(sqrt[n] A)^n=A; A geq 0$

$A^3=(sqrt[3]{8-3sqrt{21}}+sqrt[3]{8+3sqrt{21}})^3=8-3ssqrt{21}+8+3sqrt{21}+3*(sqrt[3]{8-3sqrt{21}}sqrt[3]{8+3sqrt{21}}(sqrt[3]{8-3sqrt{21}}+sqrt[3]{8+3sqrt{21}}))=16+3*sqrt[3]{(8-3sqrt{21})(8+3sqrt{21})}*A=16+3*sqrt[3]{8^2-(3*sqrt{21})^2}*A=16+3*sqrt[3]{64-189}*A=16+3*sqrt[3]{-125}*A=16-15A$

отсюда справедливо

$A^3=16-5A;\\A^3+15A-16=0; (A+1)(A^2-A+16)=0$

откуда либо $A^2-A+16=0$ , что невозможно, дискриминант отрицательный, уравнение не имеет действительных корней, а число А действительное

либо А=-1

ответ: -1

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика, автор: mahasofa

помогите пожалуйста

6 лет назад

Предмет: Алгебра, автор: ibrasevaajdana49

3.24. Ширина прямоугольника в 2 раза короче его длины. Если шири-
ну увеличить на 2 см, а длину сократить на 2 см, то площадь прямоуголь-
ника увеличится на 2 см2. Каковы измерения данного прямоугольника?

6 лет назад

Предмет: Геометрия, автор: mdaaaaaaa1200

знайдіть усі кути паралелограма якщо два його кути відносяться як 3:1

6 лет назад

Предмет: Математика, автор: Сонечка8

У Ксюши было 56 рублей.После того как она купила ручку и альбом, у нее осталось 30 рублей.Сколько стоил альбом, если ручка стоила 7 рублей?

10 лет назад

Предмет: Физика, автор: julja9098

Для ванны необходимо приготовить воду температурой 36 градусов. Из горячего крана смесителя идет вода температурой 80 градусов, а из холодного при 8 градусах. Сколько надо взять горячей воды, чтобы приготовить ванну, если для этого потребуется 196 кг холодной воды?

10 лет назад