Пожалуста помогите пожалуйста 

из центра окружности вписанной в треугольник со сторонами 13 14 15 проведена новая окружность радиуса 5 найти длины хорд отсекаемых этой новой окружность. на сторонах треугольника,  Пожалуста помогите 

см. рис во вложении

Находим радиус вписанной окружности

r=√((p-a)(p-b)(p-c)/p)

p-полупериметр

p=(13+14+15)/2=21

r=√((21-15)(21-14)(21-13)/21)=4

Из треугольника OMB находим BM

BM^2=5^2-4^2=25-16=9

BM=3

Вся хорда 2ВМ=6

Ответ 6

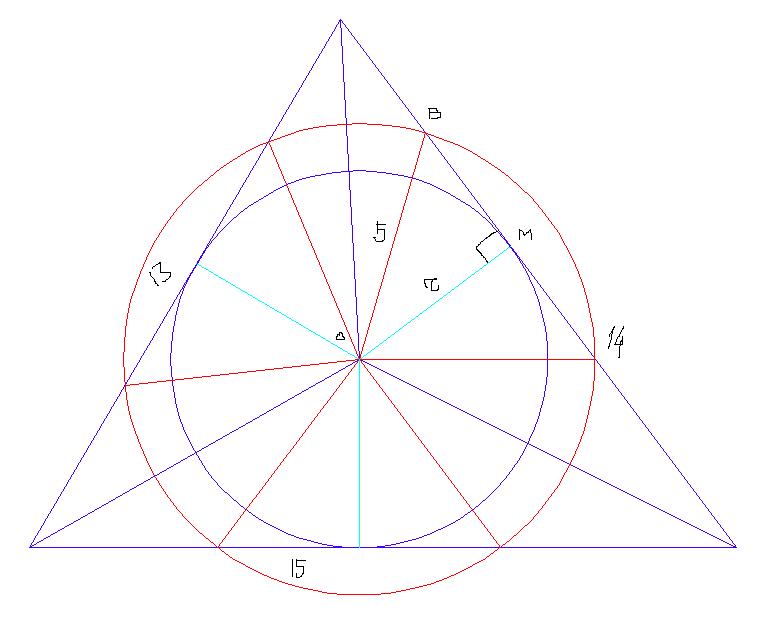
Если радиус окружности R, расстояние до хорды r, длина хорды m, то

(m/2)^2 + r^2 = R^2;

Поскольку центр окружности совпадает с центром вписанной в треугольник окружности, расстояние до искомых хорд будет одинаковым - равным радиусу вписанной окружности. То есть r -  это радиус вписанной окружности в треугольник со сторонами 13,14,15.

ПОЛУпериметр этого треугольника равен (13 + 14 + 15)/3 = 21;

Площадь треугольника легко считается по формуле Герона и равна 84. 

Этот треугольник составлен из двух Пифагоровых треугольников - со сторонами (9,12,15) и (5,12,13), приставленных друг к другу катетами 12 так, что катеты 9 и 5 вместе образуют сторону 14. Поэтому высота к стороне 14 равна 12, а площадь 12*14/2 = 84.

r = S/p = 84/21 = 4;

откуда

m/2 = 3; (здесь тоже Пифагорова тройка 3,4,5, самая первая)

m = 6; (все хорды одинаковые, само собой)