Предмет: Геометрия, автор: krutojiv

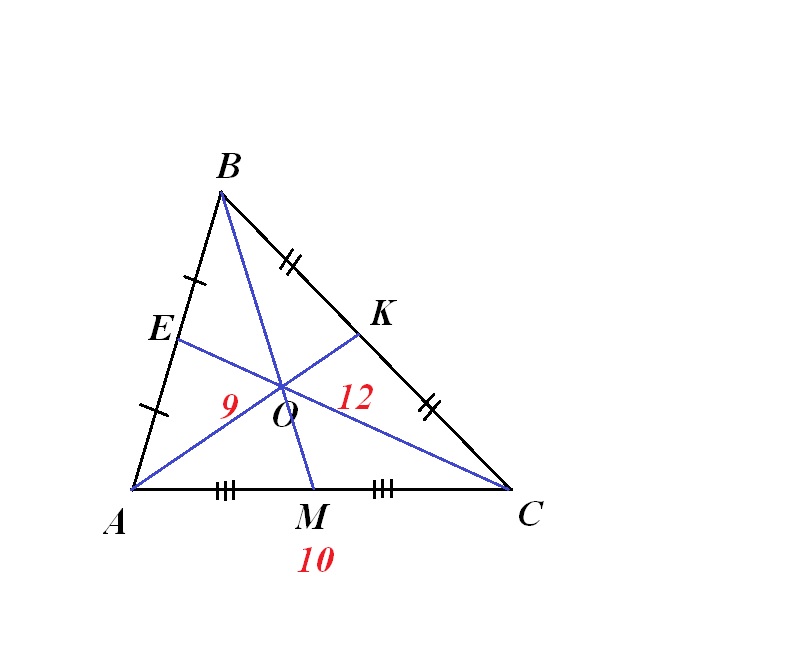
Одна из сторон треугольника равна 10, а медианы, которые проведены к двум другим сторонам, равны 9 и 12. Найти площадь треугольника

Ответы

Автор ответа: CallMeMaybe

решение смотри во вложении...

Приложения:

Автор ответа: artalex74

Чертеж во вложении.

Проведем третью медиану ВМ. Все три медианы пересекаются в одной точке О и каждая делится этой точкой в отношении 2:1:

АО:ОК=2:1, ВО:ОМ=2:1, СО:ОЕ=2:1.

Отсюда ОС=2/3СЕ=2/3*12=8, ОА=2/3АК=2/3*9=6.

Рассмотрим ∆АОС. У него ОА=6, ОС=8, АС=10.

По обратной теореме Пифагра выполняется равенство АС²=АО²+ОС² (10²=6²+8²). Следовательно, ∆АОС - прямоугольный с ∠АОС=90°.

Три медианы, пересекаясь, делят треугольник ∆АВС на 6 треугольников с равными площадями. Тогда

$S_{ABC}=6S_{AOM}=3(S_{AOM}+S_{COM})=3S_{AOC} \ S_{AOC}=frac{1}{2}AO*OC=frac{1}{2}*6*8=24 \ S_{ABC}=3*24=72$

Ответ: 72

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика, автор: galinakravchenko7

Легкоаий автомобіль був у дорозі 4 години долаючи щогодини 70 км вантажівка була в дорозі 7 годин.Скільки кілометрів щогодини долала вантажівка якщо вона проїхада на 70 км більше ніж ленковий автрмобвль

6 лет назад

Предмет: Физика, автор: artemzhuravlev2016

Длительность одного тайма футбольного матча 45 минут. Выразить эту длительность в секундах.

Можно пожалуйста с объяснением.

6 лет назад

Предмет: Қазақ тiлi, автор: blackcoconut13

Тауар өткізу,баспасөз беттері,киім-кешек,жеке кәсіп
нужно составить предложение с этими словами

6 лет назад

Предмет: Алгебра, автор: Аноним

Помогите кто чем может!

1. Турустическая группв, состаящая из 24 человек, среди которых 7 детей дошкольного возраста и 4 школьника, намерена посетить краеведчиский музей. Билет в музей стоит 60 рублей, при этомскидка для дошкольников составляет 50%, а для дошкольников -70% от стоимости билета для взрослых. Сколько всего рублей заплатит туристическая группа за билеты в музей?

2. Маяк высотой 20 м указывает на мелководье в радиусе 150 м от него. На каком расстоянии от опасной зоны находится судно, если угол повышения а, измеренный штурманом, имеет тангенс 0,1?

3. В прямоугольном треугольнике АВС угол С - 90 градусов, угол А - 40 градусов. Найдите угол между медианой и высотой, проведенными из вершины С.

Заранее спасибо)

10 лет назад

Предмет: Геометрия, автор: ZMEIZ

Найдите периметр прямоугольника, если его площадь равна 72 см в квадрате, а стороны относятся как 1:2

10 лет назад