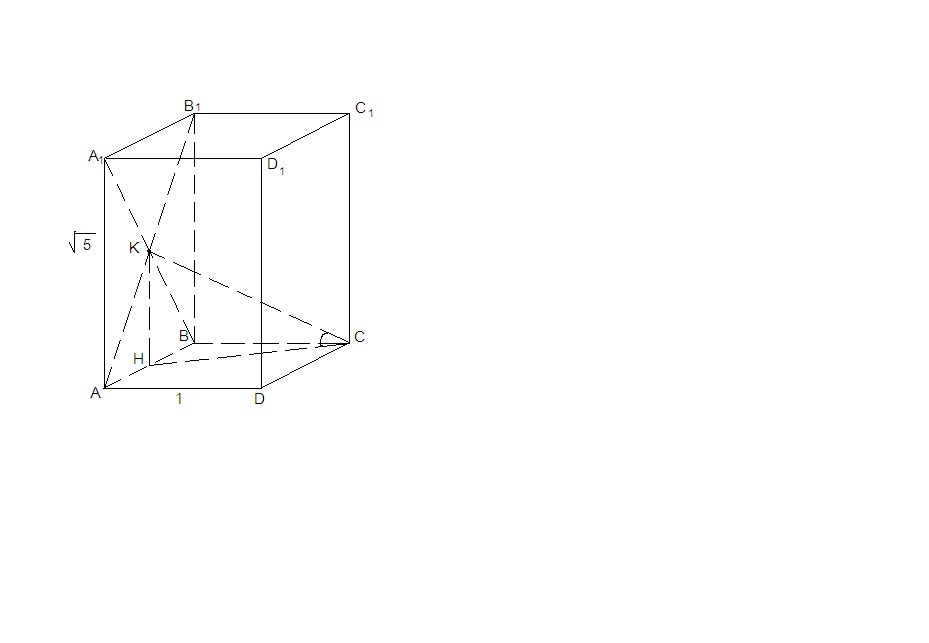
в правильной четырехугольной призме ABCDA1B1C1D1 сторона основания равна 1, а боковое ребро равно корень из 5, К-центр грани АА1В1В. Найдите угол между прямой КС и плоскостью основания.С РИСУНКОМ ПОЖАЛУЙСТА

Так как призма правильная, в основании квадрат, а боковые грани равные прямоугольники.
Пусть Н - середина АВ. Тогда КН - средняя линия ΔАА₁В,
⇒ КН ║ АА₁, КН = АА₁/2 = √5/2.
АА₁ ⊥ (ABC) ⇒ KH ⊥ (ABC) ⇒ HC -  проекция СК на плоскость основания. Значит, ∠КСН - искомый.
ΔНВС: ∠В = 90°. По теореме Пифагора:
   НС² = НВ² + ВС² = 1 + 1/4 = 5/4
   HC = √5/2
ΔKHC: ∠H = 90°. KH = HC = √5/2  ⇒ треугольник равнобедренный прямоугольный, значит, ∠КСН = 45°