Предмет: Алгебра, автор: Аноним

Помогите решить уравнения:

Приложения:

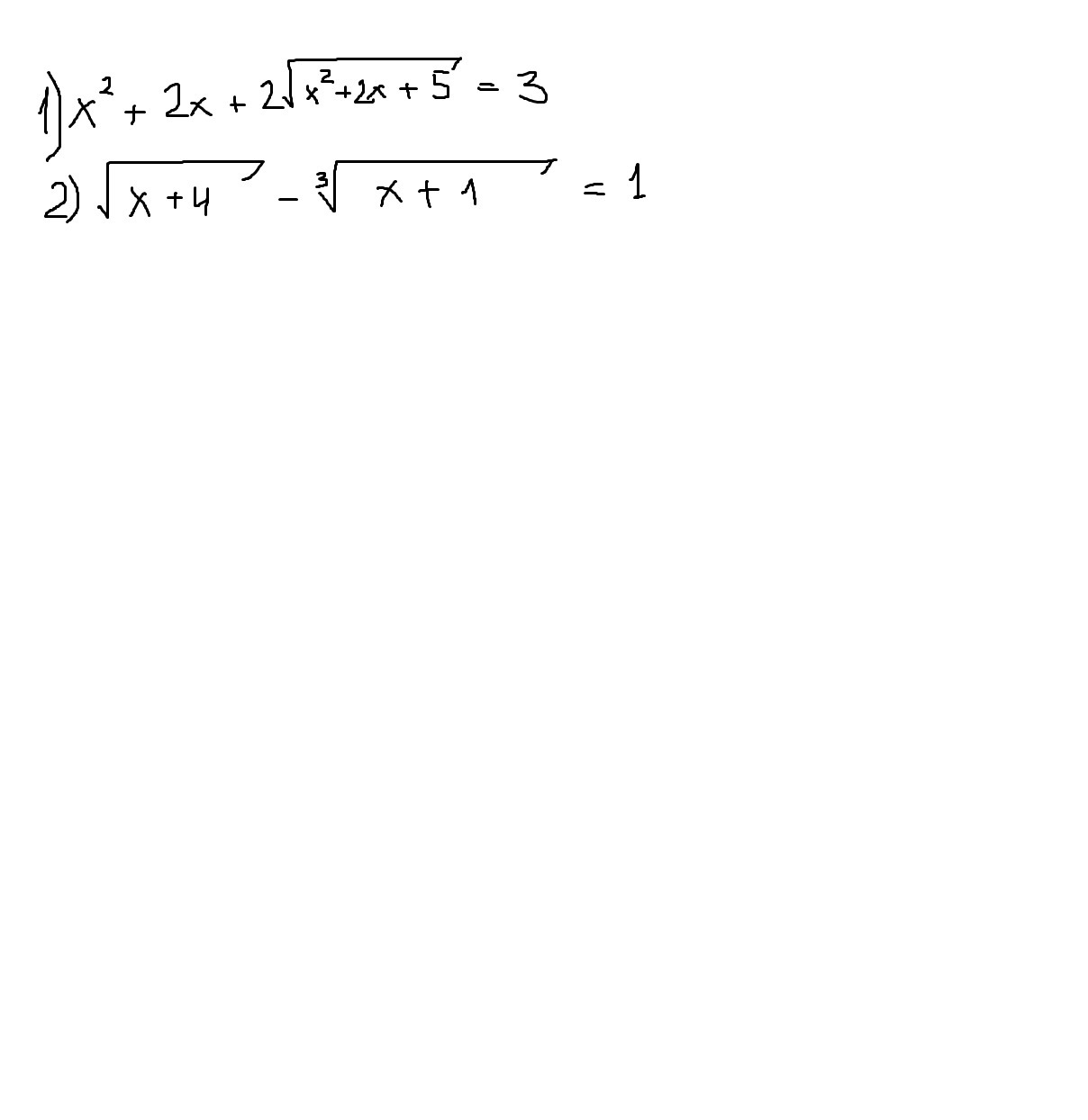
Ответы

Автор ответа: Artem112

$x^2+2x+2 sqrt{x^2+2x+5} =3 \ x^2+2x+5+2 sqrt{x^2+2x+5}+1 =3+5+1 \ ( sqrt{x^2+2x+5})^2+2 sqrt{x^2+2x+5}+1 =9 \ ( sqrt{x^2+2x+5}+1)^2 =9 \ left[begin{array}{l} sqrt{x^2+2x+5}+1 =3\sqrt{x^2+2x+5}+1 =-3end{array}$
$left[begin{array}{l} sqrt{x^2+2x+5} =2\sqrt{x^2+2x+5} =-4end{array}$
Второе уравнение не имеет решений.
$sqrt{x^2+2x+5} =2 \ x^2+2x+5=4 \ x^2+2x+1=0 \ (x+1)^2=0 \ x+1=0 \ x=-1$
Ответ: -1

$sqrt{x+4} - sqrt[3]{x+1}=1$
Обозначим:
$sqrt{x+4}=u geq 0 ; u^2=x+4 \ sqrt[3]{x+1}=v ; v^3=x+1$
Получаем систему:
$left{begin{array}{l} u^2=x+4 \ v^3=x+1 \ u-v=1 end{array}$
Из первого уравнения вычтем второе:
$left{begin{array}{l} u^2-v^3=3 \ u=v+1 end{array}$
$(v+1)^2-v^3=3 \ v^2+2v+1-v^3=3 \ v^3-v^2-2v+2=0 \ v^2(v-1)-2(v-1)=0 \ (v-1)(v^2-2)0 \ (v-1)(v- sqrt{2} )(v+ sqrt{2} )=0 \ v_1=1; u_1=1+1=2 \ v_2=sqrt{2}; u_2=sqrt{2}+1 \ v_3=-sqrt{2}; u_3=-sqrt{2}+1$
Третий случай не удовлетворяет условию $u geq 0$
$v_1=1 Rightarrow sqrt[3]{x+1}=1; x+1=1; x_1=0 \ v_2=sqrt{2} Rightarrow sqrt[3]{x+1}=sqrt{2}; x+1=2sqrt{2}; x_2=2sqrt{2}-1$
Ответ: 0 и $2sqrt{2}-1$