Предмет: Алгебра,
автор: yulyaklevakina
Помогите пожалуйста!!!!
Привести уравнение кривой второго порядка f(x;y)=0 к каноническому виду и найти точки пересечения ее с прямой Ах+Ву+С=0. Выполните графическую иллюстрацию полученного решения.
Приложения:
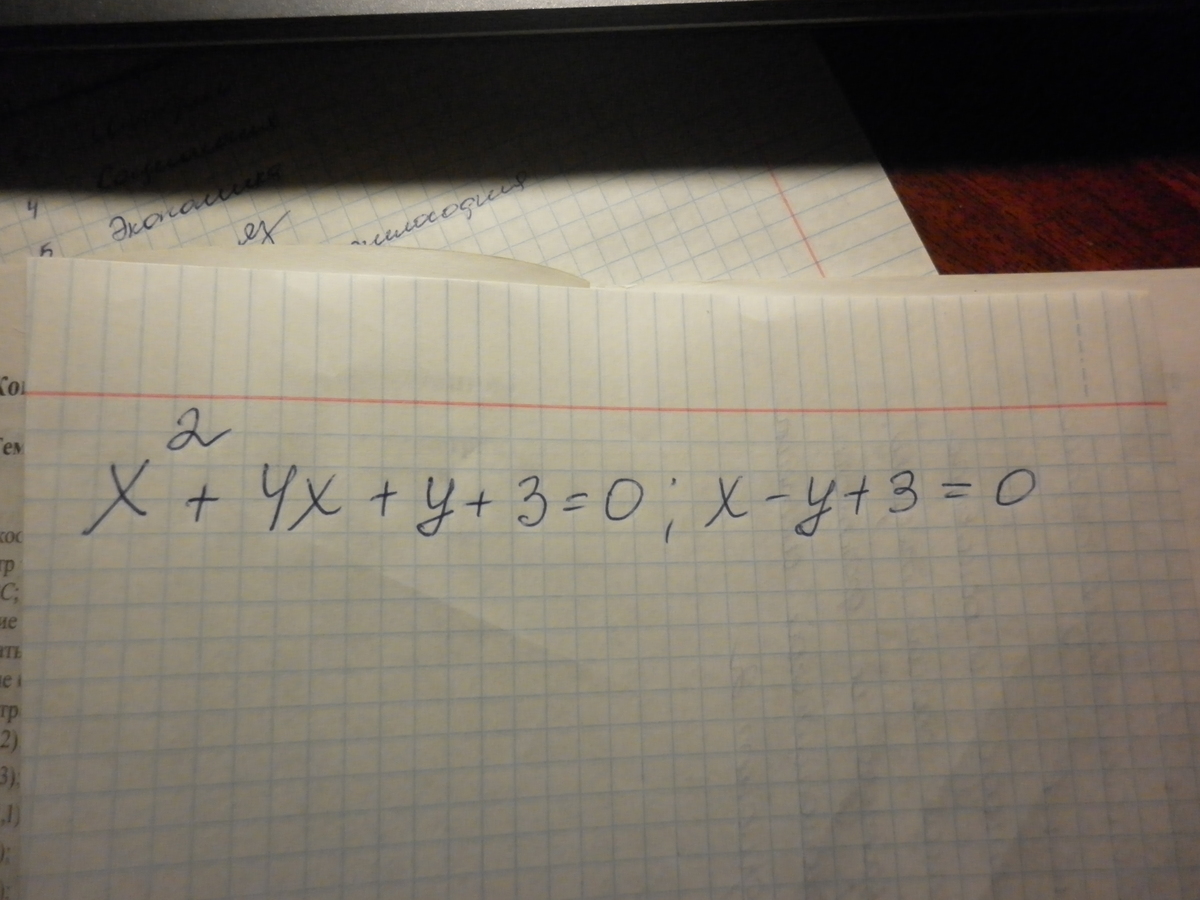
Ответы
Автор ответа:
0
1. х^2+4x+y+3=0; x^2+4x+4+y-1=0; (x+2)^2+y-1=0; y=-(x+2)^2+1 - канонический вид (парабола с вершиной в точке (-2;1) и ветками направленными вниз).
2. Найдём точки пересечения параболы и прямой х-у+3=0, решив систему уравнений методом подстановки: y=-(x+2)^2+1 и х-у+3=0; х+(x+2)^2-1+3=0; х+x^2+4х+4+2=0;
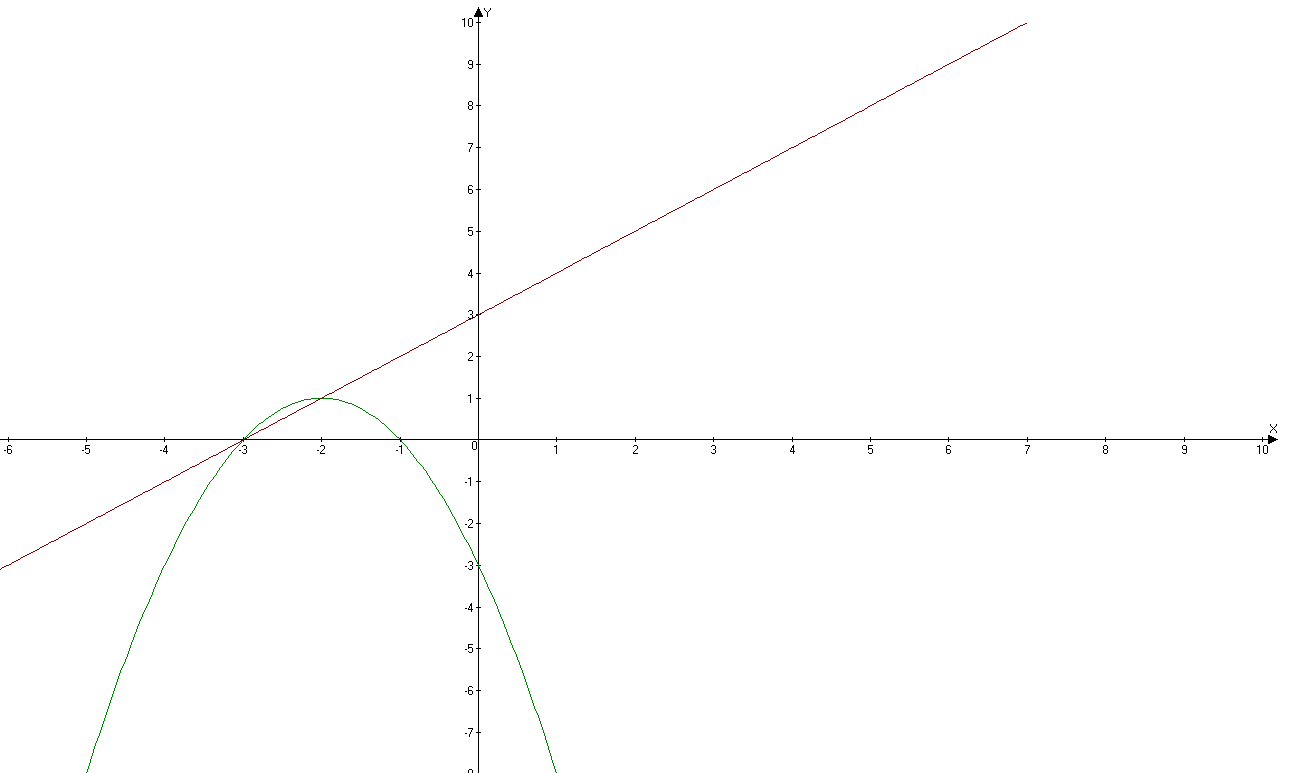
x^2+5х+6=0; х1=-3 и у1=0; х2=-2 и у2=1. (-3;0) и (-2;1) - точки пересечения параболы и прямой.
3. График во вложении
2. Найдём точки пересечения параболы и прямой х-у+3=0, решив систему уравнений методом подстановки: y=-(x+2)^2+1 и х-у+3=0; х+(x+2)^2-1+3=0; х+x^2+4х+4+2=0;
x^2+5х+6=0; х1=-3 и у1=0; х2=-2 и у2=1. (-3;0) и (-2;1) - точки пересечения параболы и прямой.
3. График во вложении
Приложения:
Интересные вопросы
Предмет: Литература,
автор: rritka194
Предмет: Математика,
автор: mt028806
Предмет: История,
автор: rusyator2003
Предмет: Обществознание,
автор: Iricha777
Предмет: Алгебра,
автор: jenese