Предмет: Геометрия,
автор: vasilenkovicto
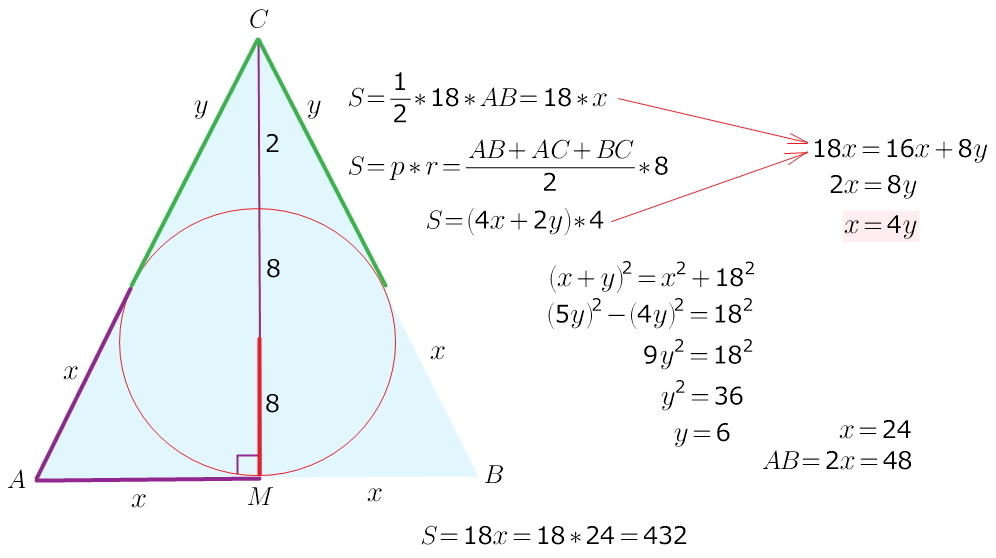
1) Высота равнобедренного треугольника, поведённая к основе, равна 18 см, а радиус вписанного круга - 8 см. Найдите площадь треугольника.
2) Основа равностороннего тупоугольного треугольника равна 18 см, а радиус описанного круга - 15 см. Найдите площадь треугольника.
Ответы
Автор ответа:
0
Замечание: равносторонний треугольник не может быть тупоугольным)))
видимо, опечатка во второй задаче...
Обе задачи очень похожи по логике решения: из двух формул для площади можно установить зависимость между сторонами треугольника или стороной и высотой треугольника и по теореме Пифагора найти нужный отрезок.
1) для любого описанного многоугольника (не только для треугольника) площадь можно вычислить через радиус вписанной окружности:
S = p * r (где p -это полу-периметр)
т.к. треугольник равнобедренный, основание разобьется на два равных отрезка (х) и отрезки касательных, проведенных из одной точки к окружности, равны)))
получим четыре равных отрезка на сторонах треугольника и еще два равных отрезка обозначим (у), осталось записать т.Пифагора...
2) здесь потребуется другая формула для площади вписанного треугольника --через радиус описанной окружности:
S = a*b*c / (4R) и т.к. треугольник тупоугольный (по условию), следовательно, тупой угол треугольника опирается на дугу окружности, которая больше 180°
видимо, опечатка во второй задаче...
Обе задачи очень похожи по логике решения: из двух формул для площади можно установить зависимость между сторонами треугольника или стороной и высотой треугольника и по теореме Пифагора найти нужный отрезок.
1) для любого описанного многоугольника (не только для треугольника) площадь можно вычислить через радиус вписанной окружности:
S = p * r (где p -это полу-периметр)
т.к. треугольник равнобедренный, основание разобьется на два равных отрезка (х) и отрезки касательных, проведенных из одной точки к окружности, равны)))
получим четыре равных отрезка на сторонах треугольника и еще два равных отрезка обозначим (у), осталось записать т.Пифагора...
2) здесь потребуется другая формула для площади вписанного треугольника --через радиус описанной окружности:
S = a*b*c / (4R) и т.к. треугольник тупоугольный (по условию), следовательно, тупой угол треугольника опирается на дугу окружности, которая больше 180°
Приложения:
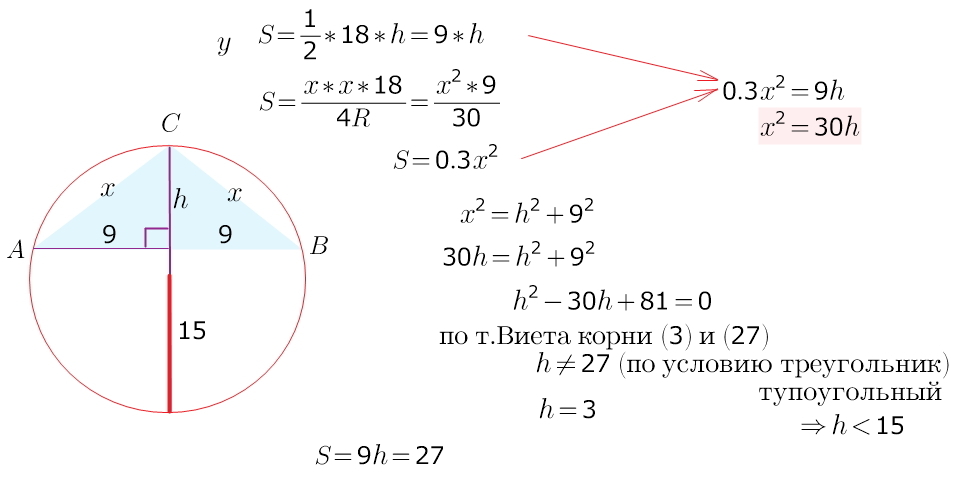
Автор ответа:
0
Спасибо огромное, чтобы я без Вас делала
Интересные вопросы
Предмет: Русский язык,
автор: aliatuganbaj
Предмет: Химия,
автор: nikitajorik3400
Предмет: История,
автор: melnicenokartem18
Предмет: Математика,
автор: Leylababayeva
Предмет: Алгебра,
автор: fedor09952