Предмет: Геометрия, автор: alinaradovnya

Касательная и секущая, выходящие из одной точки, равны соответственно
20см и 40 см. Найдите расстояние от центра окружности до секущей, если
радиус окружности равен 17см

Ответы

Автор ответа: Alphaeus

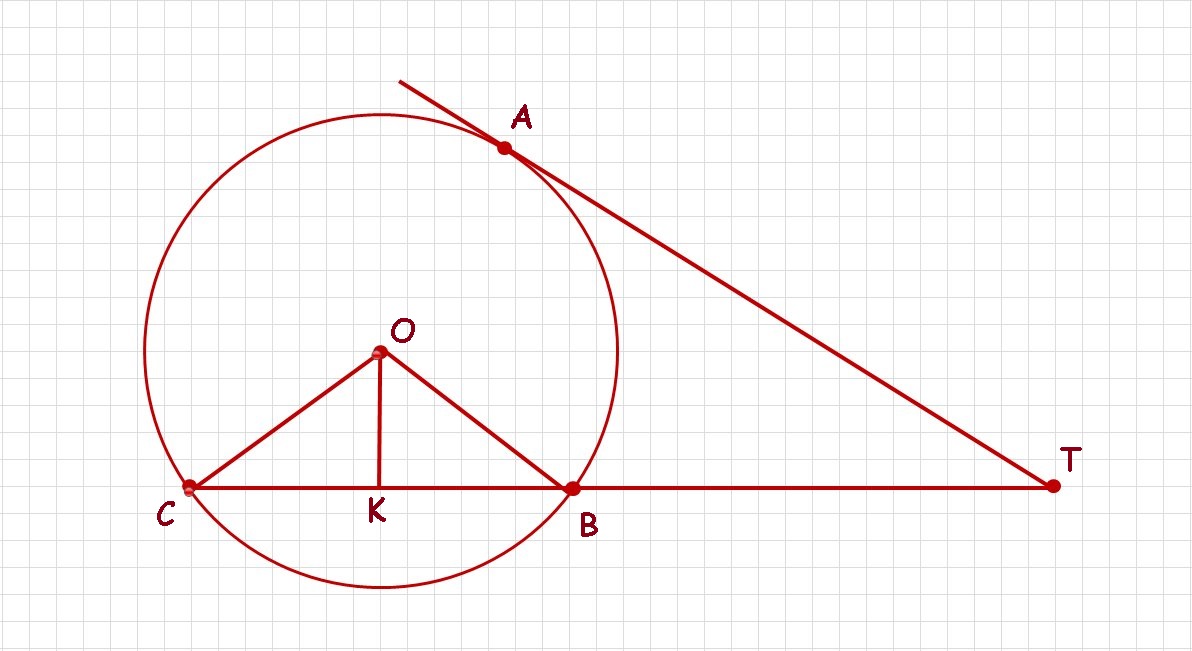
Теорема о касательной и секущей: если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной.
То есть
$TA^2 = TB*TC => TB=frac{TA^2}{TC} =frac{20^2}{40} =frac{400}{40} = 10$
ВС = ТС - ТВ = 40 - 10 = 30
Проведём перпендикуляр из точки О к отрезку секущей ВС и рассмотрим треугольник ВОС. Так как ВО = ОС = рудиусу, то треугольник равнобедренный, и значит, его высота ОК является его медианой, то есть ВК = КС = 30 / 2 = 15
Из прямоугольного треугольника ОКВ:
$OK = sqrt{OB^2 - KB^2} = sqrt{17^2 - 15^2} = sqrt{64}=8$

Ответ: расстояние от центра до секущей равно 8 см

Приложения: