Предмет: Алгебра,
автор: StailsStilinski
помогите Исследовать ряд на сходимость
Приложения:
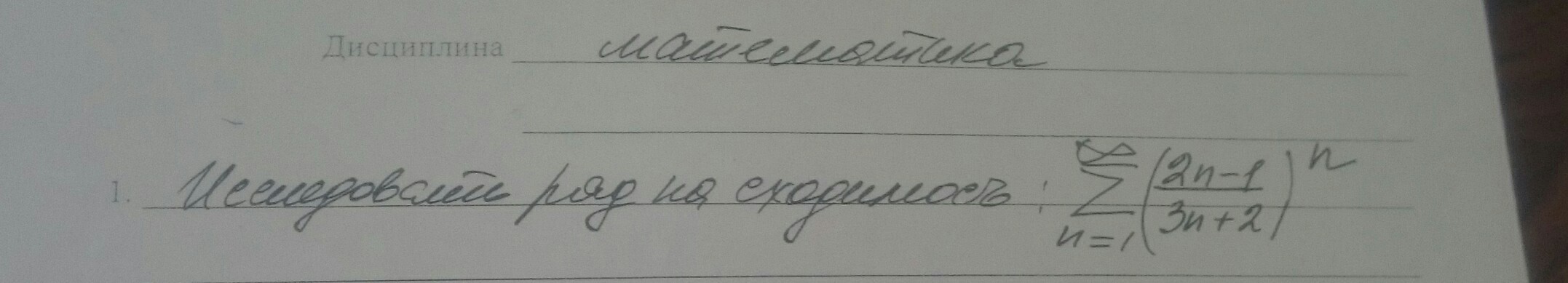
Ответы
Автор ответа:
0
Рассмотрите такой вариант:
Так как общий член ряда находится в n-степени, то наиболее эффективен для исследования радикальный признак Коши, согласно которому: если
![lim_{n to infty} sqrt[n]{a_n^n} textless 1,](https://tex.z-dn.net/?f=+lim_%7Bn+to+infty%7D++sqrt%5Bn%5D%7Ba_n%5En%7D+textless++1%2C+ "lim_{n to infty} sqrt[n]{a_n^n} textless 1,")
то ряд сходится.
![lim_{n to infty} ( sqrt[n]{ frac{2n-1}{3n+2} } )^n= lim_{n to infty} frac{2n-1}{3n+2} = frac{2}{3} textless 1](https://tex.z-dn.net/?f=+lim_%7Bn+to+infty%7D++%28+sqrt%5Bn%5D%7B+frac%7B2n-1%7D%7B3n%2B2%7D+%7D+%29%5En%3D+lim_%7Bn+to+infty%7D++frac%7B2n-1%7D%7B3n%2B2%7D+%3D+frac%7B2%7D%7B3%7D++textless++1 "lim_{n to infty} ( sqrt[n]{ frac{2n-1}{3n+2} } )^n= lim_{n to infty} frac{2n-1}{3n+2} = frac{2}{3} textless 1")
Так как предел меньше 1, значит, ряд сходится.
Так как общий член ряда находится в n-степени, то наиболее эффективен для исследования радикальный признак Коши, согласно которому: если
то ряд сходится.
Так как предел меньше 1, значит, ряд сходится.
Интересные вопросы
Предмет: Қазақ тiлi,
автор: telefondar
Предмет: Русский язык,
автор: monika200552
Предмет: Математика,
автор: Fanaka
Предмет: Математика,
автор: lysova05
Предмет: Математика,
автор: dvaletsplaychik