Предмет: Геометрия,
автор: dggshe6
ПОМОГИТЕ РЕШИТЬ ЗАДАЧУ
Приложения:
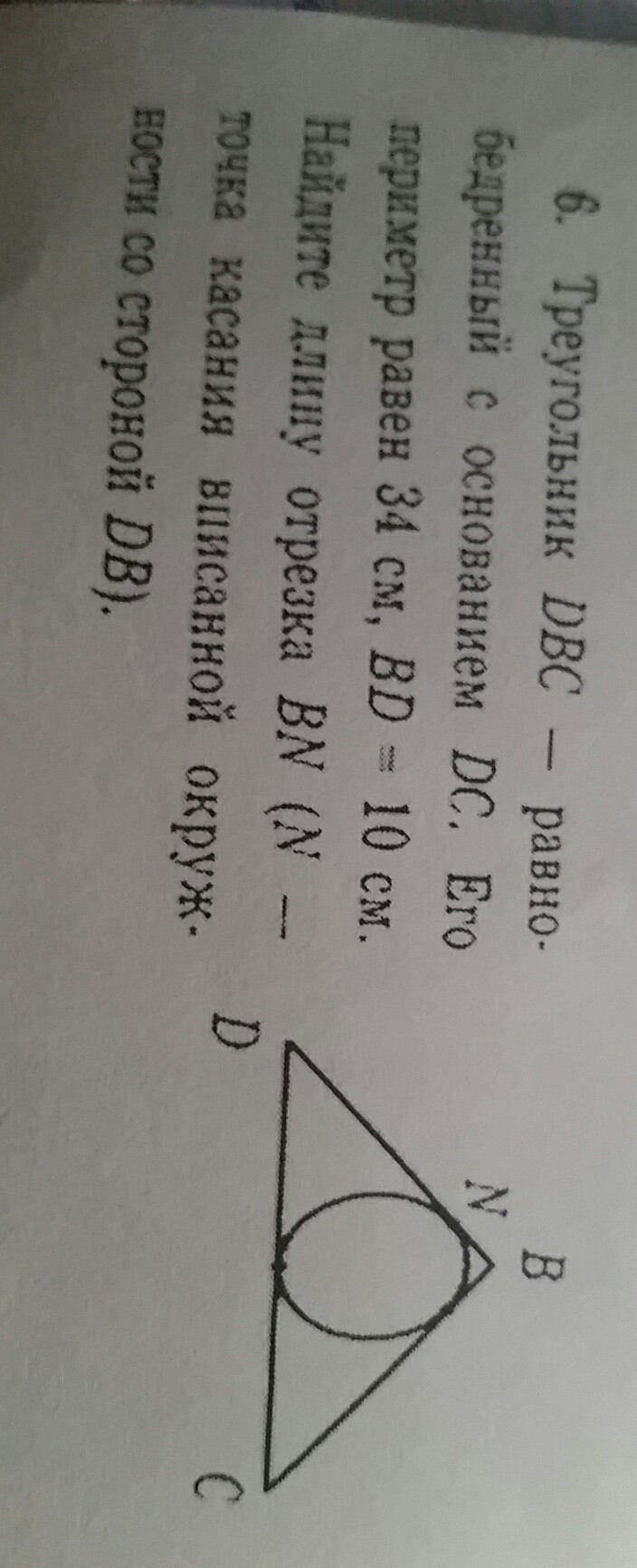
Ответы
Автор ответа:
0
Пусть окружность касается основания в точке М, а второй боковой стороны в точек Р, тогда если ND=PM=CM=CP=a (потому что треугольник равнобедренный и по теореме об отрезках касательной), а NB+BP = b,
то 34 = 4a + 2b; 10 = a + b
откуда BN = b = (a + b) - ((4a+2b)-2*(a+b))/2 = (34-2*10)/2 = 3 см.
то 34 = 4a + 2b; 10 = a + b
откуда BN = b = (a + b) - ((4a+2b)-2*(a+b))/2 = (34-2*10)/2 = 3 см.
Автор ответа:
0
получается BN мне надо найти и он равен 7
Автор ответа:
0
Да, надо найти BN? yj jy hfdty 3
Автор ответа:
0
*но он равен 3
Автор ответа:
0
почему
Автор ответа:
0
в решении написано
Автор ответа:
0
BD=10⇒BC=10⇒DC=34-10-10=14.
Пусть точка касания с основанием - точка A⇒DA=CA=DC/2-7⇒DN=7⇒ BN=BD-DN=10-7=3
Ответ: 3
Второй способ. Как известно, BN=p-DC=34/2-14=3
Пусть точка касания с основанием - точка A⇒DA=CA=DC/2-7⇒DN=7⇒ BN=BD-DN=10-7=3
Ответ: 3
Второй способ. Как известно, BN=p-DC=34/2-14=3
Автор ответа:
0
Расстояние от вершины треугольника до точки касания с вписанной окружностью равно полупериметру минус противоположная сторона
Автор ответа:
0
нет мы еще такое не прошли
Автор ответа:
0
спасибо
Автор ответа:
0
вам
Автор ответа:
0
Сделай такое задание - доказать, что расстояние... ну как у меня написано, только с рисунком, и я дам доказательство. Баллы ставь минимальные, мне они не нужны. И пришли мне ссылку
Интересные вопросы
Предмет: Физика,
автор: xawgirl
Предмет: Қазақ тiлi,
автор: leonnevidimka19
Предмет: Геометрия,
автор: v1k118
Предмет: Алгебра,
автор: Dasha77711
Предмет: Математика,
автор: а2а3а4