Предмет: Алгебра,
автор: MilkyWayyy15
Под буквой В и Г, интеграл
Приложения:
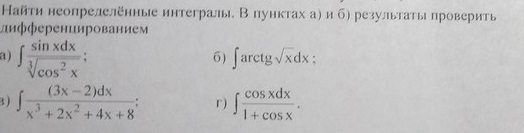
Ответы
Автор ответа:
0
Интересные вопросы
Предмет: Английский язык,
автор: pdpdpdpdpd83
Предмет: Английский язык,
автор: allapilipuk568
Предмет: Литература,
автор: katusaustimenko75
Предмет: Геометрия,
автор: Аноним
Предмет: Биология,
автор: juliasha20