Предмет: Математика, автор: lenafrolova97

Здравствуйте , помогите решить примеры по разделу" Интегральное исчисление" желательно с решением
1 Найти интегралы от рациональных функций :
∫x^4∙dx/(x^2+1)∙(x+1)
2. Найти интегралы:
∫lnx/x(1-ln^2 x) dx

Приложения:

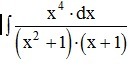
Ответы

Автор ответа: NNNLLL54

$1); ; int frac{x^4}{(x^2+1)(x+1)} dx=int (x-1+frac{1}{(x^2+1)(x+1)} )dx=I\\ frac{1}{(x^2+1)(x+1)}= frac{A}{x+1} + frac{Bx+C}{x^2+1} = frac{A(x^2+1)+(Bx+C)(x+1)}{(x^2+1)(x+1)} \\x^2; |; A+B=0; ;; ; ; B=-A\\x; |; A+B+C=0; ;; ; -2A=-C; ,; C=2A\\x^0; |; A+C=1; ;; ; 3A=1; ,; A=frac{1}{3}\\C=frac{2}{3}; ,; ; B=-frac{1}{3}\\I=int (x-1)dx+frac{1}{3}int frac {dx}{x+1}+int frac{-frac{1}{3}x+frac{2}{3}}{x^2+1} dx=$

$= frac{x^2}{2} -x+ frac{1}{3} int frac{dx}{x+1}-frac{1}{3cdot 2}int frac{2x, dx}{x^2+1} + frac{2}{3}int frac{dx}{x^2+1} = \\=frac{x^2}{2}-x + frac{1}{3}cdot ln|x+1|-frac{1}{6}ln|x^2+1|+ frac{2}{3}cdot arctgx+ C$

$2); ; int frac{lnx}{x(1-ln^2x)}dx =int frac{lnx}{1-ln^2x} cdot frac{dx}{x}=[; t=lnx; ,; dt=frac{dx}{x}; ]=\\=int frac{tcdot dt}{1-t^2}=[; u=1-t^2; ,; du=-2t, dt; ]=- frac{1}{2} int frac{du}{u} =\\=- frac{1}{2}cdot ln|u|+C=- frac{1}{2}cdot ln|1-t^2|+C=- frac{1}{2} cdot ln|1-ln^2x|+C\\P.S.; ; Moxno; srazy:; u=1-ln^2x; ,; du=-2lnxcdot frac{dx}{x}$

Автор ответа: lenafrolova97

спасибо большое

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Физика, автор: Аноним

Вода массой m = 2 кг передали количество теплоты Q = 252 кДж. на сколько градусов возросла температура воды удельная теплоемкость воды c = 4200 Дж / кг °C

6 лет назад

Предмет: Английский язык, автор: Mementomori01

Why are people fond of travelling?

6 лет назад

Предмет: Русский язык, автор: koshashinobi