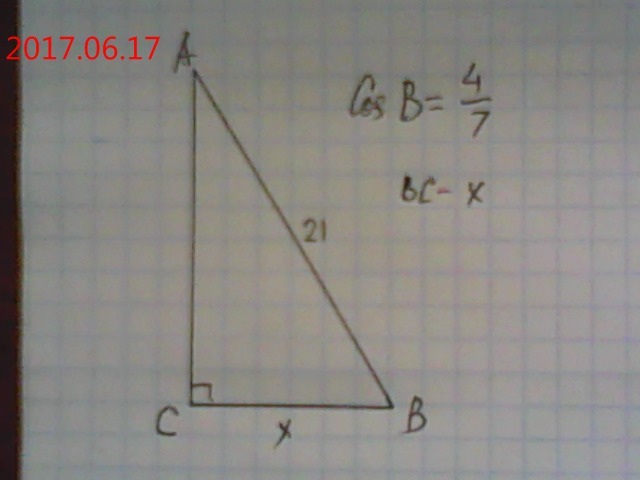
1. В треугольнике АВС угол С равен 90°, cos В равен 4/7, АВ равен 21. Найдите ВС.
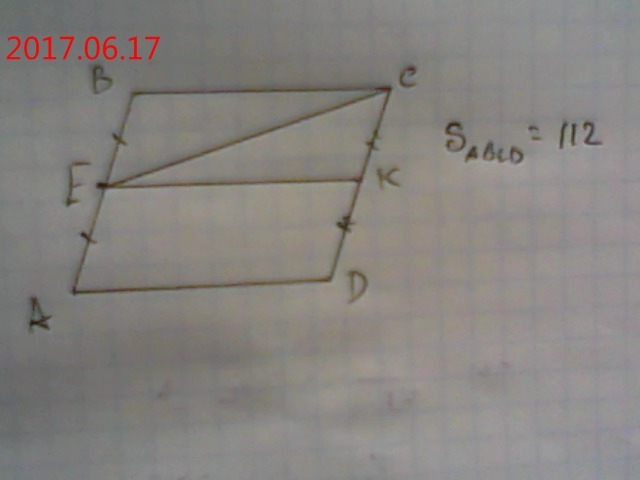
2. Площадь параллелограмма АВСД равна 112. Е - середина стороны АВ. Найдите площадь треугольника СВЕ.
Помогите, пожалуйста решить задачи. Заранее спасибо.

1) Пусть ВС=х.
sin²B+cos²B=1.
sin²B=1-cos²B=1-16/49=33/49.
sinB=√33/7.
ΔABC. sinB=BC/AB;
√33/7=x/21.
x=21√33/7=3√33.
Ответ: 3√33 л. ед.
2) Проведем ЕК║ВС. СК=DК,
ВС=ЕК=АD; ВЕ=АЕ=СК=DК.
АЕКD=ВСКЕ. Площади этих параллелограммов равны 112/2=56.
ΔВСЕ=ΔКЕС
S(ВСЕ) равен половине площади параллелограмма ВСКЕ.
S(ВСЕ)=56/2=28 кв. ед.
Ответ: 28 кв. ед.