відрізок, що сполучає центр верхньої основи циліндра з точкою кола нижньої основи, дорівнює 6см. знайдіть площу бічної поверхні циліндрп якщо його висота дорівнює діаметру основи

Отрезок, соединяющий центр верхнего основания с точкой окружности нижнего основания, равен 6 см. Найдите площадь боковой поверхности цилиндра, если его высота равна диаметру основания.

Ответ: 28,8π см²

Объяснение:  

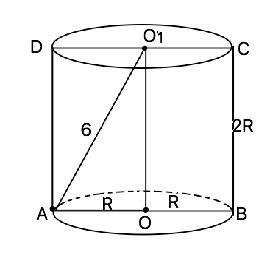
Обозначим центры оснований О и О1, точку на окружности нижнего основания - А. Отрезок, соединяющий центры оснований, перпендикулярен им и образует с радиусом нижнего основания и отрезком О1А  прямоугольный треугольник, где О1А - гипотенуза, ОО1 и ОА - катеты.

Примем радиус основания равным R, тогда диаметр АВ и высота цилиндра ВС=ОО1 равны 2R.

По т.Пифагора АО²+ОО1²=АО1²  ⇒  R²+4R²=36 ⇒  

R²=36/5, R=√(36/5)=6/√5 ⇒ H=12/√5

S(бок)=C•H=2πR•2R=4πR²

S(бок)=4π•(6/√5)²=144π/5=28,8π см²