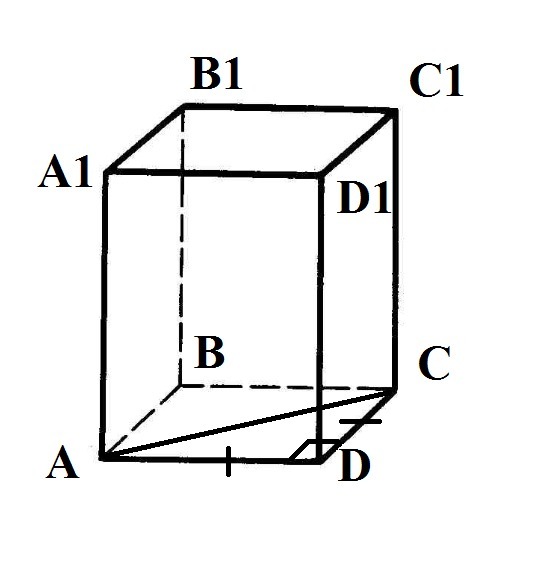
диогональ основания правильной четырехугольной призмы равна 8 корней из 2 см,а высота призмы равна 15 см. найти площадь боковой и полной поверхности призмы

Основаниями правильной четырехугольной призмы являются равные квадраты, а боковые грани - равные прямоугольники. 

Найдем сторону основания призмы через диагональ основания.

d = √2 * a, где d - диагональ квадрата, а - сторона квадрата
а = d / √2
a = 8√2 / √2 = 8 (cм)

Площадь боковой поверхности призмы
Sбок = P * h, где P - периметр основания, h - высота призмы
P = a * 4
P =8 * 4 = 32 (cм)
Sбок = 32 * 15 = 480 (cм²)

Площадь полной поверхности призмы
Sполн = Sбок + 2Sосн
Sосн = a²
Sосн = 8² = 64 (cм²)
Sполн = 480 + 2 * 64 = 608 (cм²)