найти точку минимума функции y=3(x-1,25)sinx+3cosx+2 на промежутке ( o; П2)
решите пжл

[3(x-1.25)sinx]'=3(uv)'
u=x-1.25  u'=1   v=sinx   v'=cosx
(uv)'=u'v+v'u=1*sinx+(x-1.25)cosx
y'=3sinx+3xcosx-3.75cosx-3sinx=cosx(3x-3.75)
критические точки cosx=0  x=π/2+πn  ∉  (0;π/2)
3x=3.75   x=1.25
    0<1.25<π/2≈1.57   1.25∈(0;π/2)  ymin(1.25)=3cos1.25+2

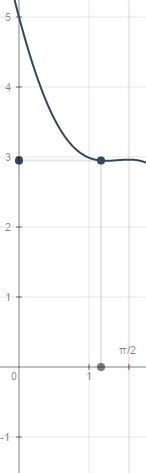
для четкости график.