Предмет: Алгебра,
автор: CTARIY
Решить систему уравнений с четыремя неизвестными.... Мой мозг не осиливает. Надо найти какие-нибудь значения ΧΥΑb
Приложения:
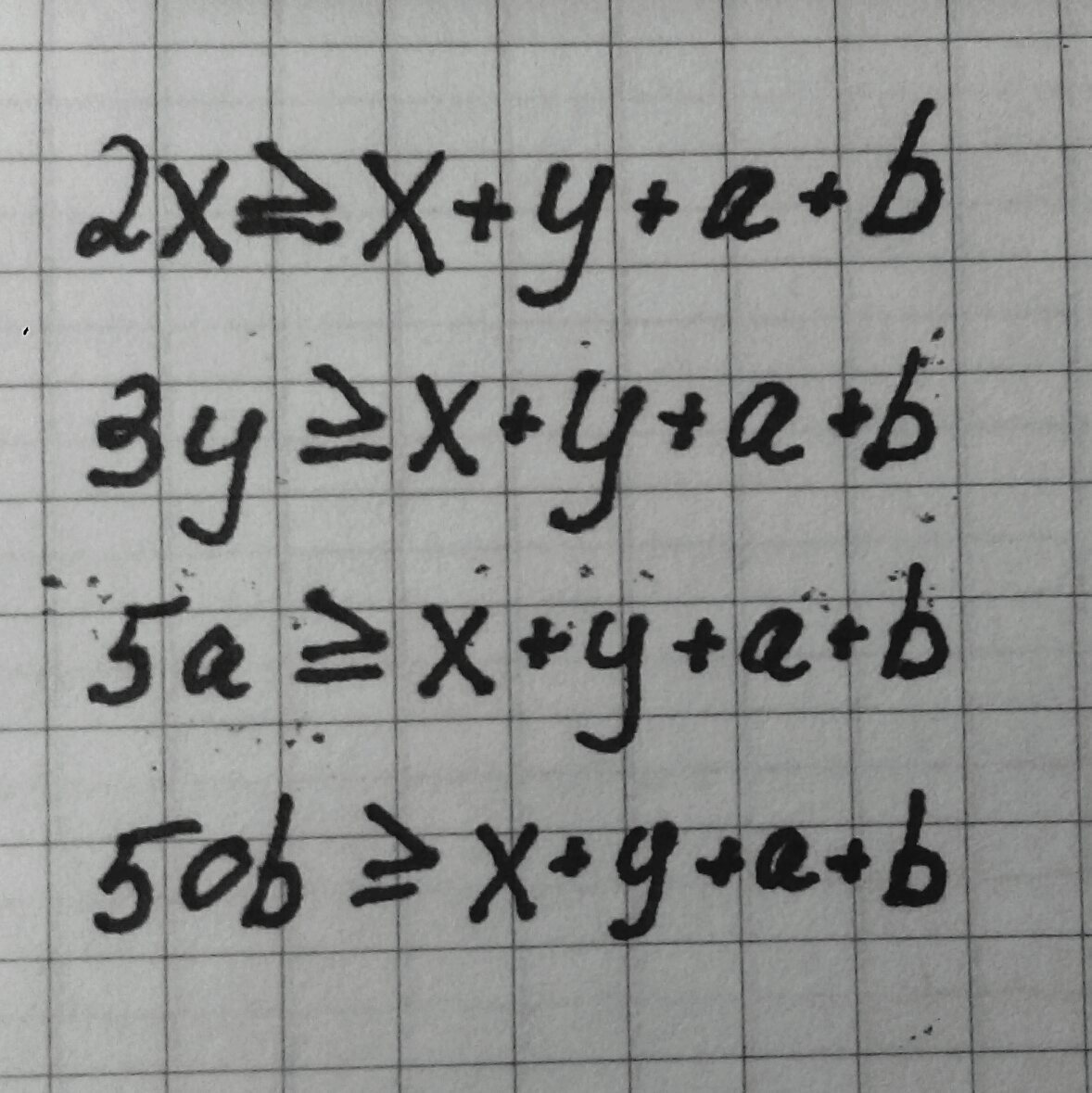
Ответы
Автор ответа:
0
Раз нужно найти "какие-нибудь" значения, то можно просто решить систему уравнений:
Решим методом Гаусса:
Составим и упростим (приведем к ступенчатому виду) матрицу состоящую из коэффициентов данной системы.
![displaystyle left[begin{array}{cccc}-1&1&1&1\1&-2&1&1\1&1&-4&1\1&1&1&-49end{array}right] xrightarrow{R_i+R_1,forall iinmathbb N:1 textless i leq 4} left[begin{array}{cccc}-1&1&1&1\0&-1&2&2\0&2&-3&2\0&2&2&-48end{array}right]\\xrightarrow{R_i+2R_2,forall iinmathbb N:2 textless i leq 4} left[begin{array}{cccc}-1&1&1&1\0&-1&2&2\0&0&-1&6\0&0&6&-44end{array}right]\\xrightarrow{R_4+6R_3}left[begin{array}{cccc}-1&1&1&1\0&-1&2&2\0&0&-1&6\0&0&0&-8end{array}right]](https://tex.z-dn.net/?f=displaystyle+++left%5Bbegin%7Barray%7D%7Bcccc%7D-1%26amp%3B1%26amp%3B1%26amp%3B1%5C1%26amp%3B-2%26amp%3B1%26amp%3B1%5C1%26amp%3B1%26amp%3B-4%26amp%3B1%5C1%26amp%3B1%26amp%3B1%26amp%3B-49end%7Barray%7Dright%5D+xrightarrow%7BR_i%2BR_1%2Cforall+iinmathbb+N%3A1+textless++i+leq+4%7D++left%5Bbegin%7Barray%7D%7Bcccc%7D-1%26amp%3B1%26amp%3B1%26amp%3B1%5C0%26amp%3B-1%26amp%3B2%26amp%3B2%5C0%26amp%3B2%26amp%3B-3%26amp%3B2%5C0%26amp%3B2%26amp%3B2%26amp%3B-48end%7Barray%7Dright%5D%5C%5Cxrightarrow%7BR_i%2B2R_2%2Cforall+iinmathbb+N%3A2+textless++i+leq+4%7D+left%5Bbegin%7Barray%7D%7Bcccc%7D-1%26amp%3B1%26amp%3B1%26amp%3B1%5C0%26amp%3B-1%26amp%3B2%26amp%3B2%5C0%26amp%3B0%26amp%3B-1%26amp%3B6%5C0%26amp%3B0%26amp%3B6%26amp%3B-44end%7Barray%7Dright%5D%5C%5Cxrightarrow%7BR_4%2B6R_3%7Dleft%5Bbegin%7Barray%7D%7Bcccc%7D-1%26amp%3B1%26amp%3B1%26amp%3B1%5C0%26amp%3B-1%26amp%3B2%26amp%3B2%5C0%26amp%3B0%26amp%3B-1%26amp%3B6%5C0%26amp%3B0%26amp%3B0%26amp%3B-8end%7Barray%7Dright%5D "displaystyle left[begin{array}{cccc}-1&1&1&1\1&-2&1&1\1&1&-4&1\1&1&1&-49end{array}right] xrightarrow{R_i+R_1,forall iinmathbb N:1 textless i leq 4} left[begin{array}{cccc}-1&1&1&1\0&-1&2&2\0&2&-3&2\0&2&2&-48end{array}right]\\xrightarrow{R_i+2R_2,forall iinmathbb N:2 textless i leq 4} left[begin{array}{cccc}-1&1&1&1\0&-1&2&2\0&0&-1&6\0&0&6&-44end{array}right]\\xrightarrow{R_4+6R_3}left[begin{array}{cccc}-1&1&1&1\0&-1&2&2\0&0&-1&6\0&0&0&-8end{array}right]")
![displaystyle xrightarrow{R_4to frac{1}{8}R_4}left[begin{array}{cccc}-1&1&1&1\0&-1&2&2\0&0&-1&6\0&0&0&-1end{array}right]](https://tex.z-dn.net/?f=displaystyle+xrightarrow%7BR_4to++frac%7B1%7D%7B8%7DR_4%7Dleft%5Bbegin%7Barray%7D%7Bcccc%7D-1%26amp%3B1%26amp%3B1%26amp%3B1%5C0%26amp%3B-1%26amp%3B2%26amp%3B2%5C0%26amp%3B0%26amp%3B-1%26amp%3B6%5C0%26amp%3B0%26amp%3B0%26amp%3B-1end%7Barray%7Dright%5D "displaystyle xrightarrow{R_4to frac{1}{8}R_4}left[begin{array}{cccc}-1&1&1&1\0&-1&2&2\0&0&-1&6\0&0&0&-1end{array}right]")
Отсюда:
Правда данное решение можно увидеть сразу, или использовать трюк. Но я решил использовать метод Гаусса.
Решим методом Гаусса:
Составим и упростим (приведем к ступенчатому виду) матрицу состоящую из коэффициентов данной системы.
Отсюда:
Правда данное решение можно увидеть сразу, или использовать трюк. Но я решил использовать метод Гаусса.
Интересные вопросы
Предмет: География,
автор: akulaakulaa026
Предмет: Биология,
автор: frizenzhen78
Предмет: Физика,
автор: udyaroshenko
Предмет: Математика,
автор: мария582