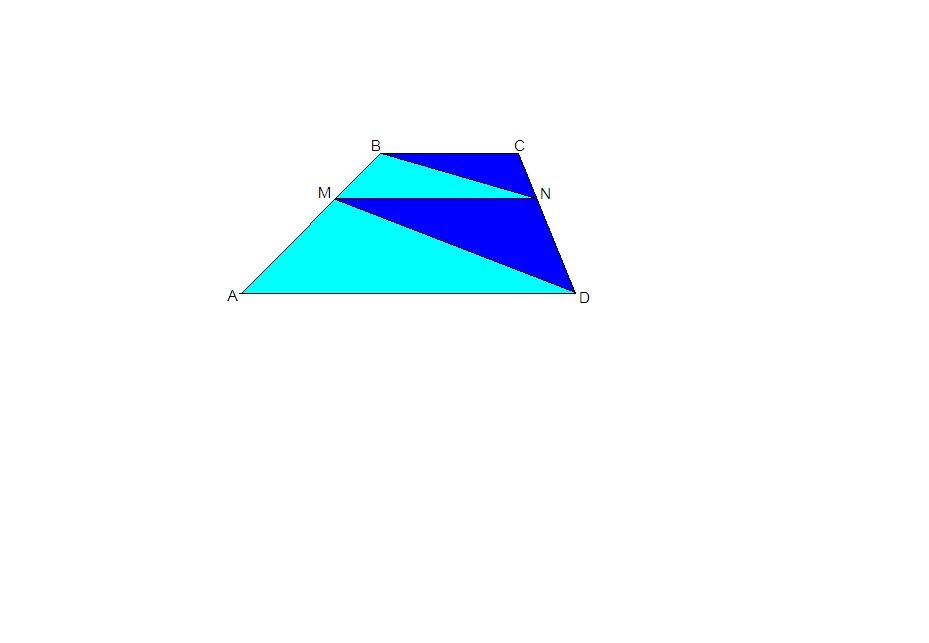
На боковых сторонах AB u CD трапеции АВСД отмечены,соответственно , точки М u N, так что АМ:М:В=5:3 и прямая MN паралельна оснаваниям AD u BC.Найдиту длину меньшего основания трапеции,если длина большего основания AD=25, BN||MD

Т.к. MN ║ AD, то CN:ND = AM:MB = 5:3
∠BAD = ∠BMN как соответственные при пересечении MN ║ AD секущей AB.
∠AMD = ∠ABN как соответственные при пересечении MD ║ BN секущей AB.
Тогда ΔAMD подобен ΔMBN по двум углам.
AD/MN = AM/MB
25/MN = 5/3
MN = 15
 
∠CDM = ∠CNB как соответственные при пересечении MD ║ BN секущей CD.
∠DNM = ∠DCB как соответственные при пересечении MN ║ BC секущей CD.
Значит, ΔMND подобен ΔBCN по двум углам. Значит,
MN/BC = DN/NC
15/BC = 5/3
BC = 9