постройте график функции y=(x^2-3x)|x-5|/x-3 и определите при каких значениях m прямая y=m имеет с графиком три общие тоочки

y=(x^2-3x)|x-5|/(x-3)
   (x^2-3x)abs(x-5)/(x-3)


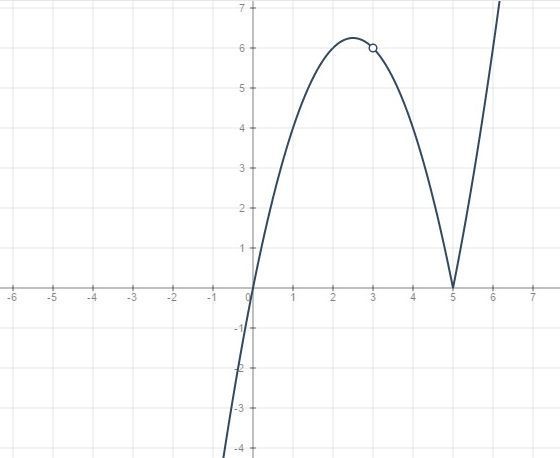
x≥5  y=x(x-3)(x-5)/(x-3)   x≠3   y=x(x-5) корни  x=5
y=x²-5x   y'=2x-5=0   x=2.5  не подходит
-------------------------------------2.5---------
                           ↓                      ↑

x<5     y=x(5-x)  корни x=0
y=-x²+5x   y'=-2x+5=0  2x=5
x=2.5     точки экстр.
-----------------------------------2,5-----------5
            ↑                                      ↓
                                       y(2.5) max