Предмет: Алгебра,
автор: roshangold3
Найдите площаь треугольника, ограниченного осями координат и касательной к графику функции y=3/x в точке с абсциссой x(внизу)0=1/3
Ответы
Автор ответа:
0
Касательная задается уравнением:
y(кас) = f ’(x0) · (x − x0) + f (x0)
Здесь f ’(x0) — значение производной в точке x0, а f (x0) — значение самой функции. Xo=1/3
y = 3/x, y(1/3) = 3/(1/3) = 9.
y' = -3/x², y'(1/3) = -3/(1/9) = -27.
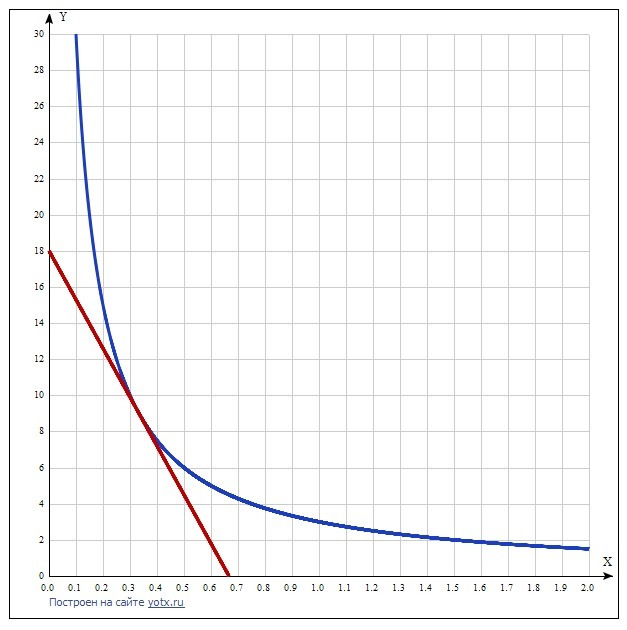
у(кас) = -27(х - (1/3)) + 9 = -27х + 9 + 9 = -27х + 18.
Точки на осях:
Ох: у = 0, -27х + 18 = 0, х = 18/27 = 2/3.
Оу: х =0, у = 18.
S = (1/2)(2/3)*18 = 6 кв.ед.
Приложения:
Интересные вопросы
Предмет: История,
автор: mata08042010
Предмет: Математика,
автор: artemsmirnov10062012
Предмет: Алгебра,
автор: 5gc7nrtv7b
Предмет: Математика,
автор: Annalshdmd
Предмет: Французский язык,
автор: Antifreeze1111