Предмет: Алгебра, автор: kanafievrafael

Помогите пожалуйста решить

Приложения:

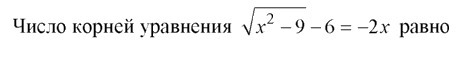
Ответы

Автор ответа: drwnd

$x^2-9 \geq 0; x \geq 3, x \leq -3$
$\sqrt{x^2-9} =6-2x$
$x^2-9=36-24x+4x^2$
$3x^2-24x+45 =0$
$x^2-8x+15=0$
$D=64-60=2^2$
$x_{1} = \frac{10}{2} =5$
$x_{2} = \frac{6}{2} =3$

оба корня удовлетворяют условиям ОДЗ, но в школьной практике мы работает с арифметическими корнями. При х=5, выражение $\sqrt{5^2-9} = \sqrt{16} = б4$
данному уравнению удовлетворяет только алгебраический(!) корень " $-4$ ", но его мы рассматривать не можем, а при $\sqrt{5^2-9} = \sqrt{16} = + 4$ условие равенства не выполняется. Поэтому корень уравнения х=5 не подходит.
Таким образом: ответ х=3, 1 корень

Автор ответа: sedinalana

√(x²-9)=6-2x
ОДЗ
{(x-3)(x+3)≥0⇒x≤-3 U x≥3
{6-2x≥0⇒2x≤6⇒x≤3
\\\\\\\\\\\\\\\ ////////////
---------[-3]-------------[3]------
/////////////////////////////////
x∈(-∞;-3] U {3}
возведем в квадрат
x²-9-36+24x-4x²=0
3x²-24x+45=0
x²-8x+15=0
x1+x2=8 U x1*x2=15
x1=3
x2=5∉ОДЗ
Ответ 1 корень

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Физика, автор: Milashka548

Напиши умови проведення електричного струму як фізичного явища.

1 год назад

Предмет: Математика, автор: rrr838757

Розв‘яжіть рівняння |x|=-1,6, пожалуйста скажите

1 год назад

Предмет: Музыка, автор: planshetsoni2021

Построить || 7 в тональности ля мажор и соль мажор! Срочно, пожалуйста помогите!!!

1 год назад

Предмет: Українська мова, автор: 0967210112s

Складним із сполучниковим і безсполучниковим зв'язком є речення *

1.Сонце заходить, гори чорніють,пташечка тихне, поле німіє.
2.Плачуть дощі в снігах, просять вітри спочину і розбивають в прах зоряну павутину.
3.Ранок був безвітряний, тихо пролітала негуста пороша,садок ніби відпочивав.
4.Планета сива над віками крутиться, минають дні, і пахне сіножать.

7 лет назад

Предмет: Русский язык, автор: STAR1331

ДАМ 10 БАЛЛОВ!
ЧЕМ ОТЛИЧАЕТСЯ подлежащее от существительного,а сказуемое от глагола!?

7 лет назад